課題 下流物体がロケットエンジン流れに与える影響 背景 　現在のロケットにはベル型ノズルと呼ばれる形状のロケットノズルが使用されている．このノズルは図1の様になめらかな曲線で設計されている．しかしこのノズルは周囲圧の影響で膨張比が制限されるという欠点がある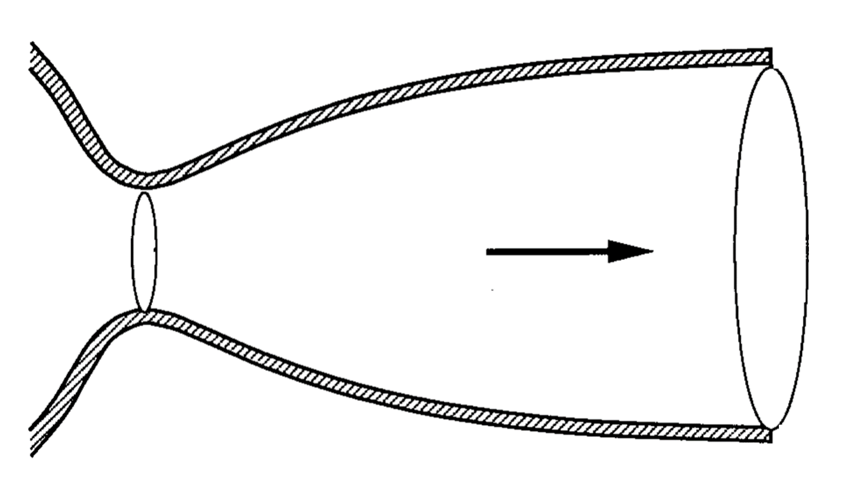． Fig.1. ベル型ノズル模式図. 　そこで考案されているのがデュアルベルノズルと呼ばれる形状である．これは図2の様にベル型ノズルを軸方向につなげた形状となっている．低高度では流れが変曲点の部分で剥離することで，通常のベル型ノズルと同様の流れとなり，高高度では周囲圧が減少することで流れが大きく膨張し，高い推力を生み出すことが出来る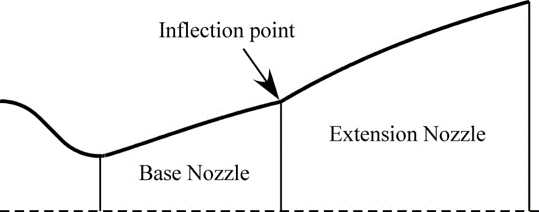． Fig.2. デュアルベル型ノズル模式図. 　デュアルベルノズルは主に単段式ロケットへの採用が期待されている．しかし，前述した通り幅広い高度に適用できる事から，再使用ロケットへの適用も検討されている．この場合，打ち上げ，着陸時には過膨張流れになる事が想定される．しかし，下流物体がデュアルベルノズル内の流れに与える影響はいまだ少ない． 　よって本研究では，デュアルベルノズルを用いた垂直離着陸を想定し，下流物体がノズル内の流れに与える影響を調べた， 目的 　本研究では，下流物体が過膨張時のデュアルベルノズル内流れに与える影響を調べる為，実験と数値計算の両方を調べる 方法 　下流物体に衝突した流れはノズル方向に跳ね返る事で，ノズル内流れに三次元的な影響を与える事が予想される．今回はまず，下流物体が無い場合のデュアルベルノズルの三次元計算を行った．図3に今回使用した計算格子を示す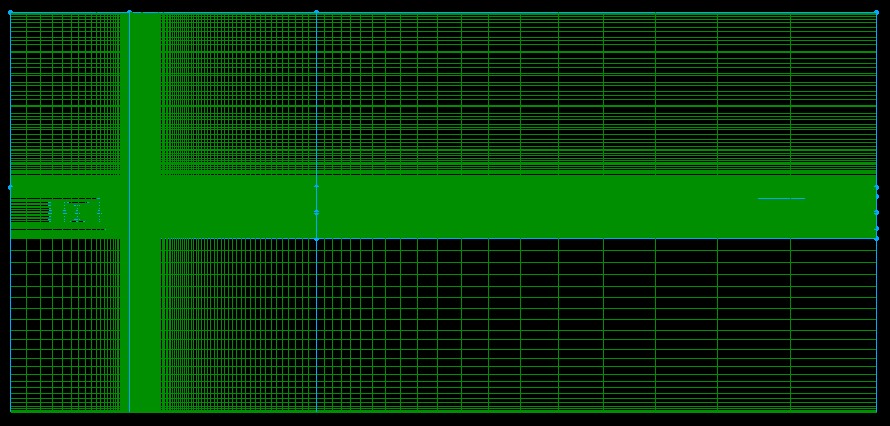． (a) 計算格子の全体図. 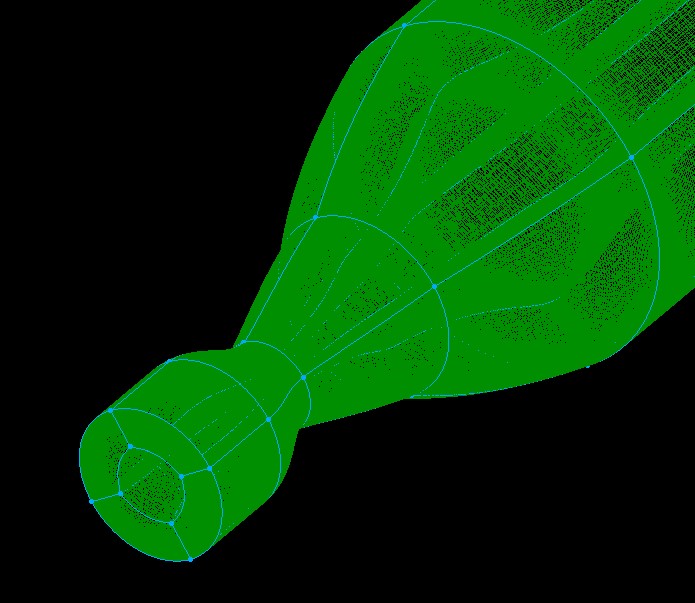(b) 計算格子ノズル拡大図. Fig.3. 三次元軸対称計算に用いた計算格子. 　今回比較のために，二次元軸対称計算と常温の空気を用いた実験の結果も併せて記載する．よって図4に二次元軸対称計算に用いた計算格子，図5に実験装置の概略図を示す． (a) 計算格子の全体図. (b) 計算格子ノズル拡大図. Fig.4. 二次元軸対称計算に用いた計算格子. 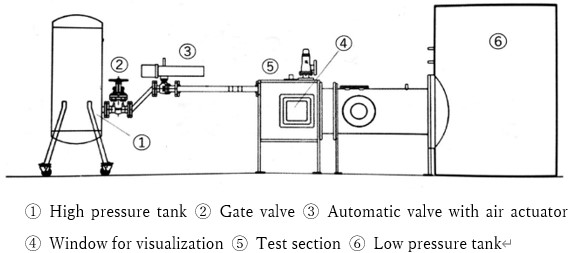Fig.5. 実験装置の概略図. 結果 　壁面圧力の計測点を図6に示す．実験，二次元計算，三次元計算でx，y座標に違いはない．また，実験と三次元計算ではz=0かつy>0となる点を計測点とした．図7，図8にそれぞれA点とB点での壁面圧力変化を示した．壁面圧力は背圧で割ることで無次元化した．横軸のNPRとは，入り口全圧を背圧で割った無次元数である．壁面圧力が単調増加し始めたNPRを剥離点が計測点を通過したNPRとした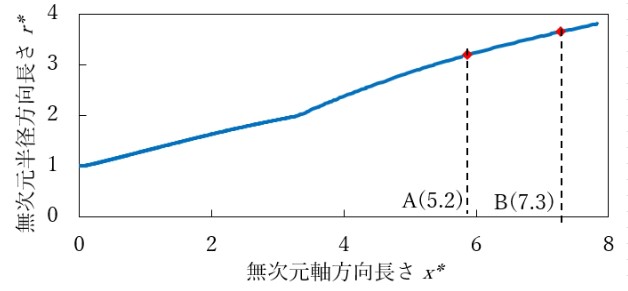． Fig.6. 壁面圧力計測点. 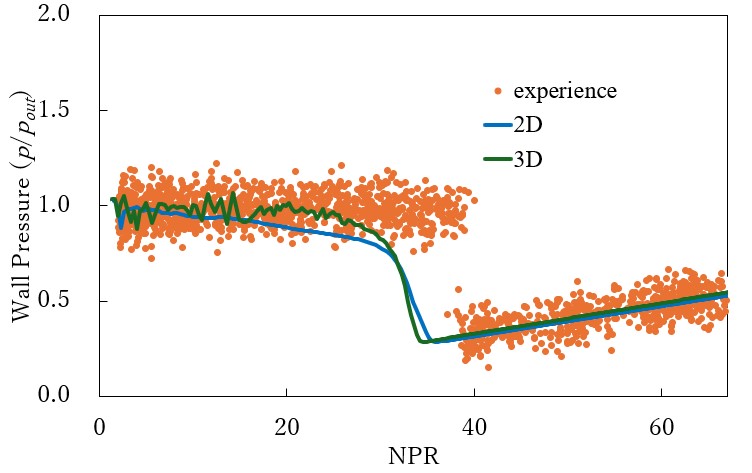Fig.7. A点での壁面圧力変化. 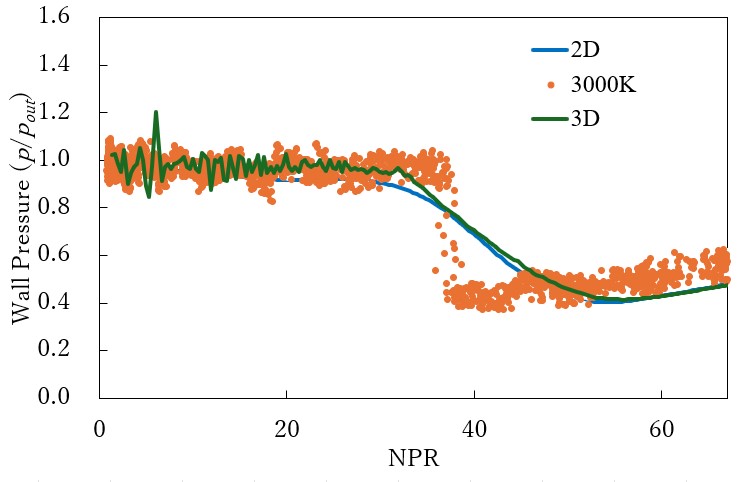Fig.8. B点での壁面圧力変化. 　図7と図8より，二次元計算と三次元計算の結果を比較すると，A点とB点のどちらでも剥離点の移動したNPRに違いは見られなかった．しかしNPRが20以下の時，三次元計算では圧力変動が起こった．これは，三次元計算では，二次元計算では見られない三次元的な流れの変化が起きたからだと考えた． 　また，実験値と数値計算の結果を比較すると，剥離点が通過したNPRに差が出ている事が分かる．これは，実験装置に使用したダクトが小さいため，一度ノズルから出た流れが再度ノズル内に侵入し，剥離点に影響を与えたからだと考えた(図9)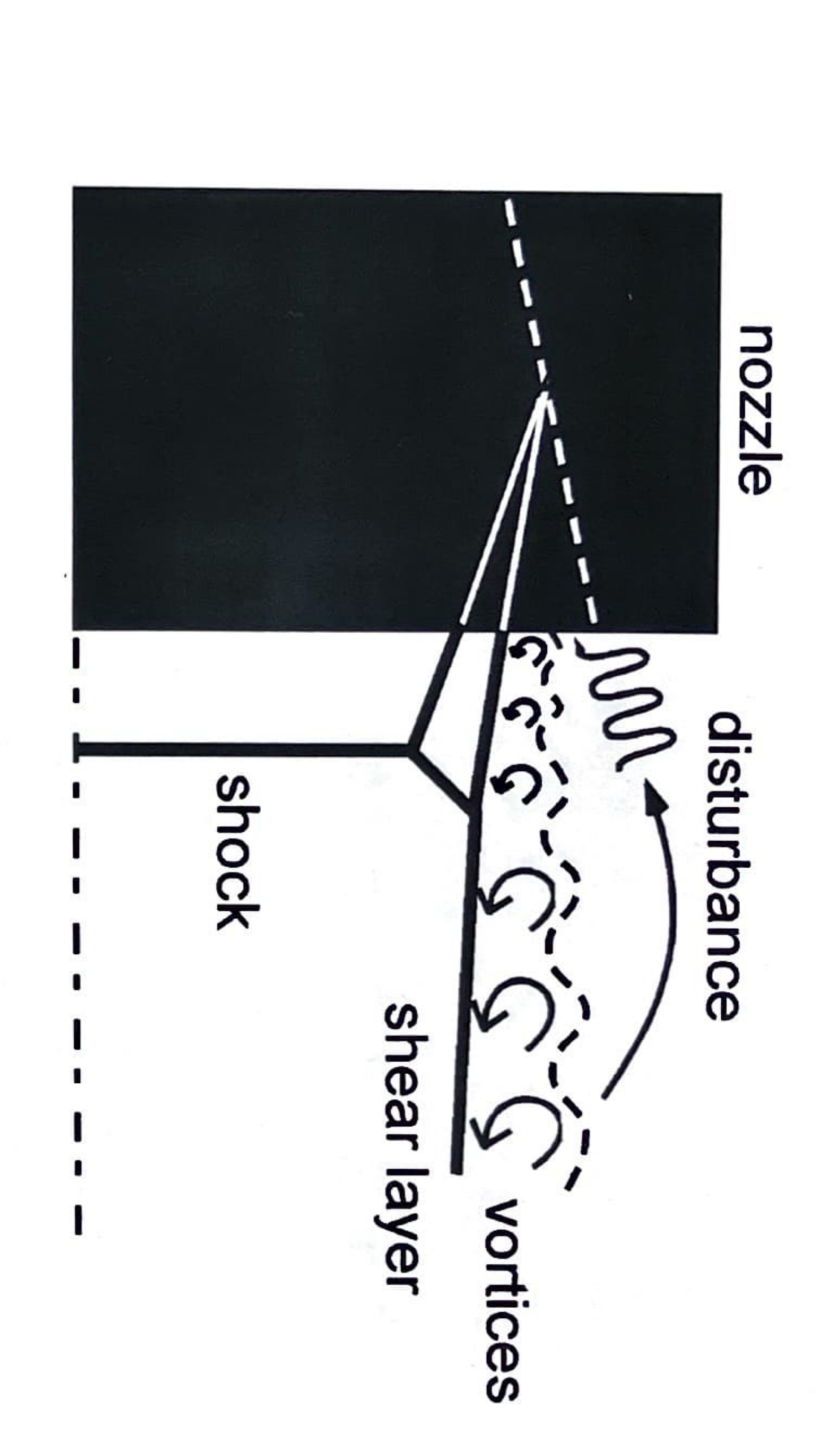． Fig.9. 剥離点の周辺の模式図.