課題 プラズマアクチュエータ 背景 　近年，小型で軽量な電気流体デバイスとしてプラズマアクチュエータ(以下：PA)が注目されている．PAは，電気流体力学的作用により，雰囲気気体の流れを誘起する流体制御デバイスである．羽根車やモータなどの機械的可動部が不要な単純な構造をしている点で従来のデバイスと比べて優れている． PAには放電形式として，誘電体バリア放電を用いたものと，コロナ放電を用いたものの2種類がある． 　誘電体バリア放電式のPAは，誘電体バリア放電式プラズマアクチュエータ，通称DBD-PA(Dielectric Barrier Discharge Plasma Actuator)と呼称され，電極構造は2枚のシート状の電極で誘電体を挟んだものとなっており，小型で平坦な形状をしている．構造物に貼り付けることで剝離低減等の効果があり，航空機翼における剝離の抑制を始めとした多くの研究例がある．ただし欠点として，誘電体の消耗による寿命の短さが挙げられる． 　一方で，コロナ放電式のPAは，コロナ放電式プラズマアクチュエータ，通称CD-PA(Corona Discharge Plasma Actuator)と呼称され，陽極と陰極の形状が非対称であり，片方が鋭利な形状をしていればよいため，電極形状の自由度が高い．これまでのコロナ放電を利用したデバイスは，EHDポンプ，回転式アクチュエータなどが存在し，針対垂直平板系の駆動機構，針対円筒系の流路，電気集塵機などが挙げられる．同じ出力において，DBD-PAと比べて強い流れを誘起することができ，過去の研究では，針電極の針先の曲率半径が小さい程流速が速いことが明らかになっているが，3次元的な構造でのみ安定した流速が得られることから，構造物への設置が難しいという課題がある． 　そこで，構造物への設置が容易である2次元的な形状をしたCD-PAとして，電極に注射針を用いたデバイスを開発した．針先端が壁面から浮いているため，デバイスを構造物に設置しても流れを誘起することができ，コロナ放電を用いた強い流れの誘起と壁面設置の両立が可能である． Figure 1. 針型CD-PA. 目的 　本研究では，電極として針を用い，壁面設置が可能である新型のCD-PAの誘起流を最大化することを目的とし，PIVを用いて誘起流の速度分布を取得することで，電極の並列化の可否，および電極配置が誘起流に及ぼす影響について調査した．また，CFDを用いて流れの可視化を行い，数値解析の妥当性評価を行った． 方法 <実験方法> 　本実験で使用したCD-PAのデバイス構成を図2に示す．図2のように，CD-PAの電極には，陰極として注射針を，陽極として銅テープを用い，2本の注射針を並列つなぎで設置した．また，下壁面には絶縁体であるポリイミドテープを用い，このデバイスをアクリル板に張り付けて使用した．針の材質はステンレス鋼，銅テープは銅製であり，針電極は直径1 mm，角度約18°のものを用い，銅テープは厚さ0.07 mm，幅20 mmのものを用いた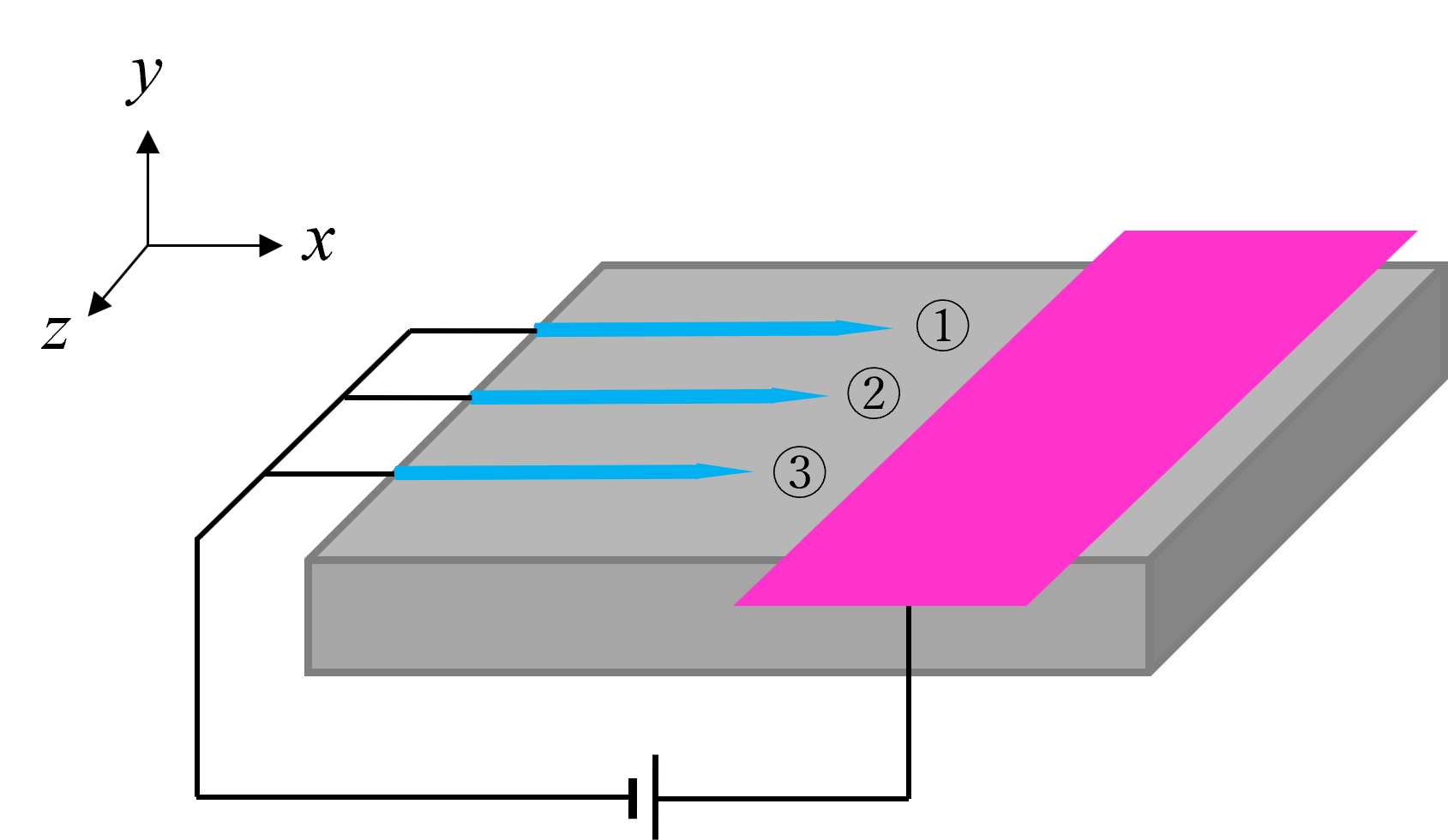． Figure 2. CD-PAの電極構成. 　続いて，図3に実験装置全体の概略図を示す．測定位置における流れ場でPIV(Particle Image Velocimetry)計測を行うことで，流れ場の速度ベクトルを求め，CD-PAの流れ場解析を行った．アクリル製のボックス内にPAを設置し，容器内をトレーサー粒子で十分に満たした．次にレーザーシート光を測定位置に照射した．アクリルボックス内に充満しているトレーサー粒子にレーザー光が反射し，その反射光を可視化することで流速計測が出来る．可視化した断面はハイスピードカメラを使用し，5,000 fpsの設定で0.1秒間（500枚）撮影を行った．トレーサー粒子にはグリコール系溶液を加熱したスモークを用いており，トレーサー粒子の粒子径は約10 μm，密度は20 ℃において1.040 kg/m3である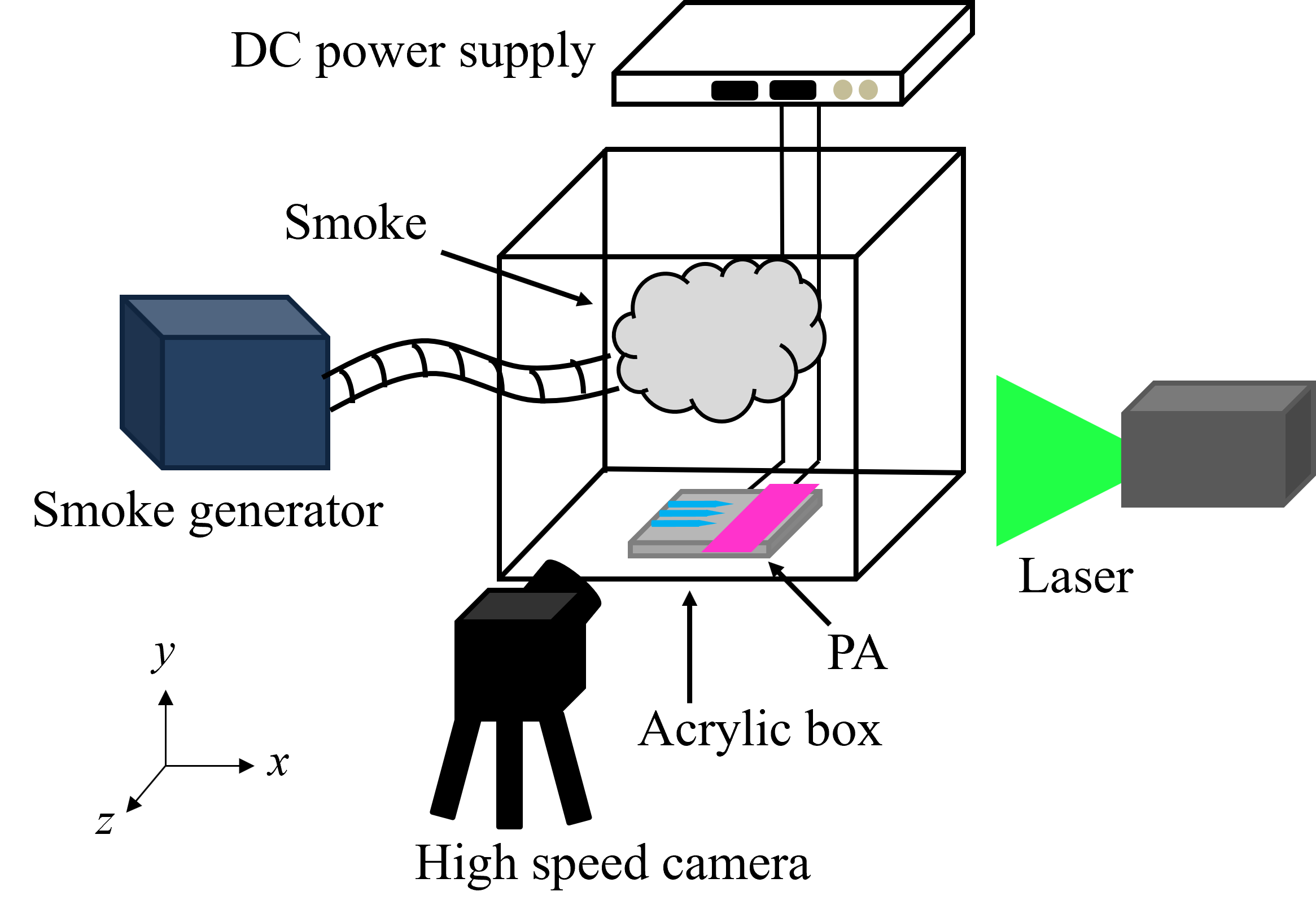． Figure 3. 実験装置全体の概略図. 　本実験では，針電極を2本と3本用いた場合について，並列に設置した際の流れ場を調査した．針と銅テープの距離は5 mm，印加電圧は5 kVとした．針を2, ３本用いた場合では，図１中の最も奥にある電極①をz = 0 mmとし，レーザーの照射位置を1 mmずつ変化させ実験を行った． <数値計算方法> 　数値計算で設定した境界条件を図4に示す．数値計算にはANSYS CFX 2024 R1を使用し，3次元定常計算を行った．流体に関する支配方程式としてナビエストークス方程式，電磁場に関する支配方程式としてマクスウェル方程式を用いた．これらの方程式を用い電磁場流体計算を行った．壁面はすべて滑りなしの条件とし，図3のように，針電極を接地，平板電極を5 kVに設定し，その他下壁面は電流値を0とした．なお，計算領域は自由流入境界とし，電極間距離は5 mmである．また，電離した空気の電気伝導度σを以下の式(1)のように定義した． 　　　　　　　　　　　　　σ=1/(1+e^(-ax) )×b+10^(-9) [S/m]　　　　　　　　　　　(1) 　針電極先端をx=0とし，パラメータa,bを変化させ計算を行った．計算結果を実験結果と比較することで，本モデルの妥当性を評価した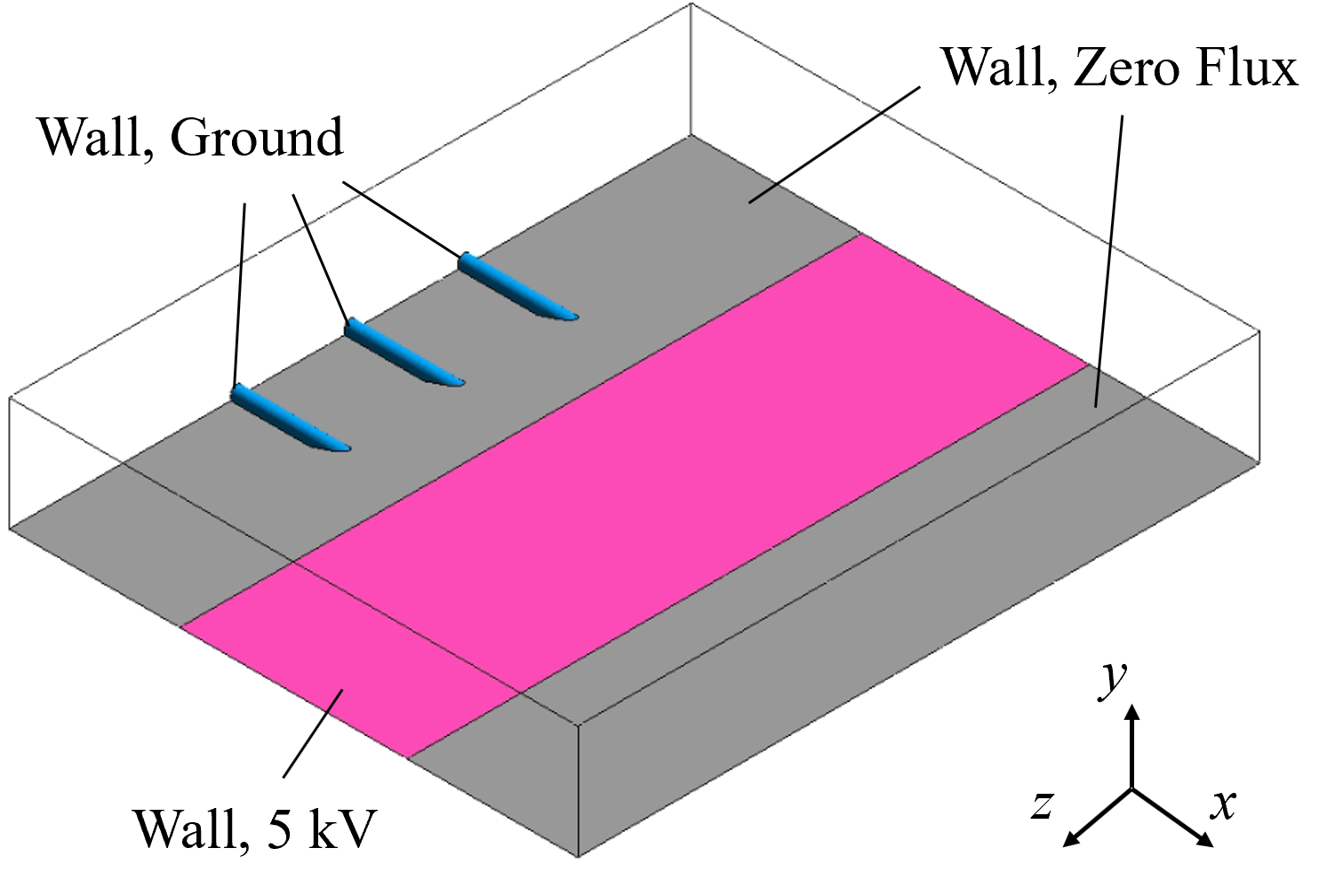． Figure 4. 境界条件. 結果 <実験結果> 　針を3本用いて並列化した針型CD-PAにおいて，w=5 mmとした場合のPIV結果を時間平均し，図5に示す．ただし，片端の電極上をz=0 mm，両端の中心に位置する電極上をz=5 mm，もう一端の電極上をz=10 mmとし，可視化断面は針電極間を1 mm間隔ごととした． 　図4より，すべての可視化位置において，針電極先端付近で最も流速が大きい．また，針電極上での流速が最も大きくなっており，中心に位置する針電極に近づくにつれ徐々に小さくなっていき，壁面に沿わない流れになっていることが確認できる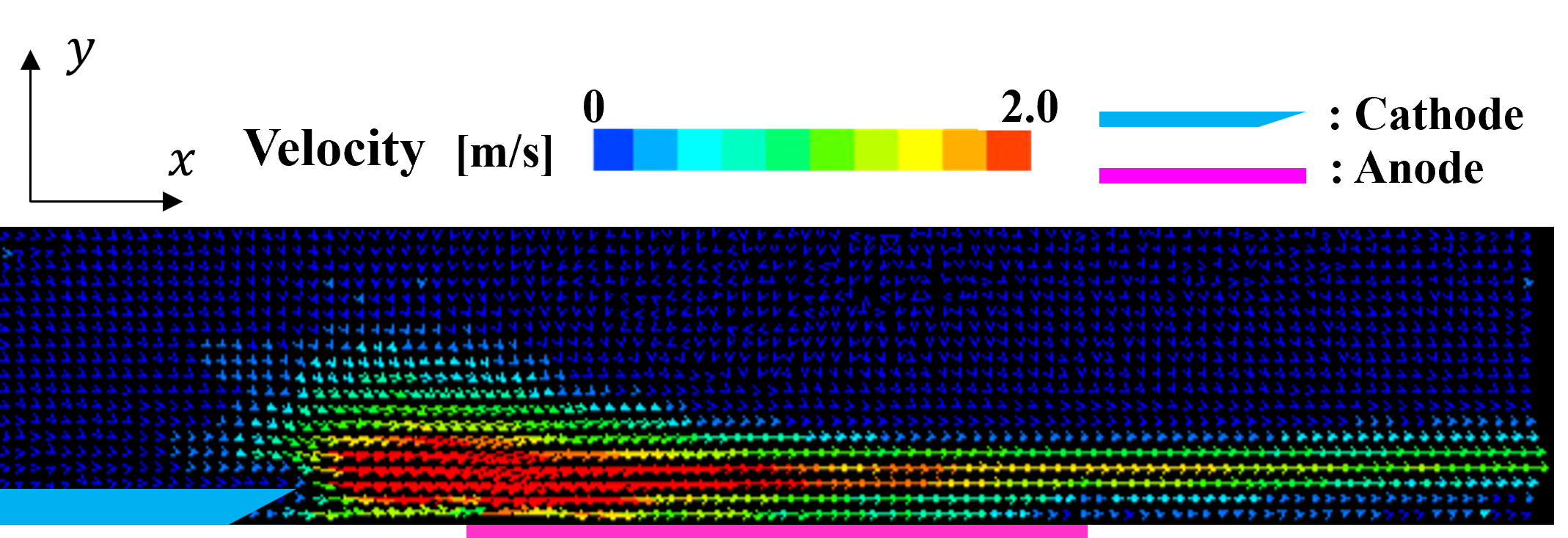． (a) z = 0 mm (b) z = 1 mm (c) z = 2 mm (d) z = 3 mm (e) z = 4 mm 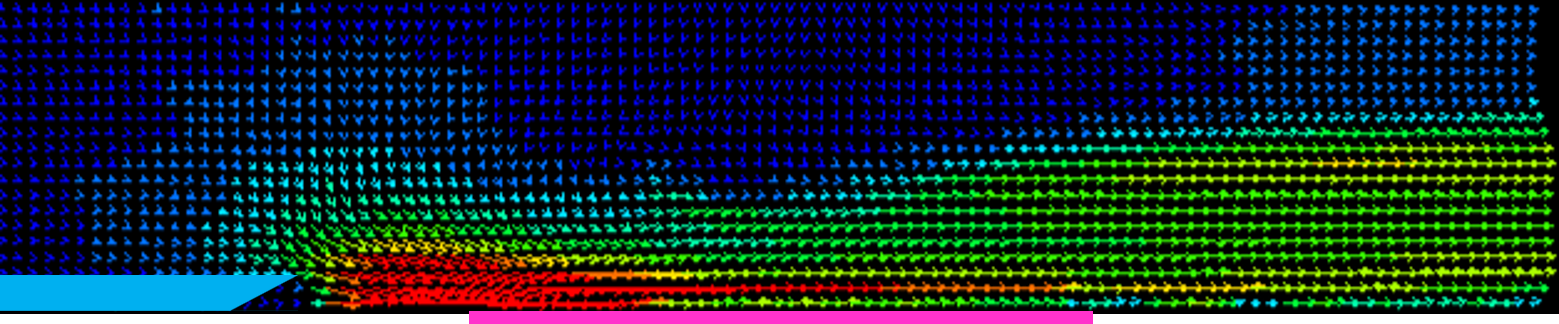(f) z = 5 mm Figure 5. 針電極を3本用いた場合のPIV結果. 　続いて，本CD-PAにおいて，x方向からの撮影を行い，500枚撮影を行った中の１枚を流れ(粒子)の様子として図6に示す．ただし，可視化断面は，針電極の先端をx = 0 mmとしたときのx = 20 mmの位置とし，青い丸印は針電極の位置を表している． 　図6より，針電極上に渦が存在していることが確認できる．この渦は，3つの針電極から誘起される流れの干渉によるものであると考えられ，これによって針電極間の中心から見た左右での流速と流量の差，および壁面に沿わない流れが引き起こされていると考えられる．また，w=5 mmとしたとき，針を2本用いた場合では渦が生じなかったが，針を3本用いた場合では渦が生じたことから，両端の針電極間の距離が渦の発生に起因していると考えられる． Figure 6. 渦の様子. 　針を2本と3本用いて並列化を行った針型CD-PAにおいて，並列化を行う前との比較を行う．ここでは，針間隔w=5 mmの場合について比較する． 　各z方向位置における可視化断面について流量を算出し，比較したものを図7に示す．ここで，流量の算出方法は，ある位置における流速ベクトルに微小面積である0.5×1 mm2を掛け，y方向に積分を行った． 　図7より，針電極上ではすべての針の本数において非常に似た流れを誘起しており，ほとんど同じ流量が得られている．針電極上から離れると，針を２本用いた場合は１本用いた場合よりも流速が小さくなっているが，これは，２本の針電極から誘起される流れの干渉であると考えられる．また，針電極上から離れるほど，針を２本用いた場合の方が流量が多い．さらに，針を３本用いた場合は，渦の影響により針電極上から離れた位置では壁面に沿わない流れが生じたものの，全体的に流量が多く，針２本を用いた場合と比べても流量が多いことから，針を複数本用いても性能を低下させることなく並列化できることが示された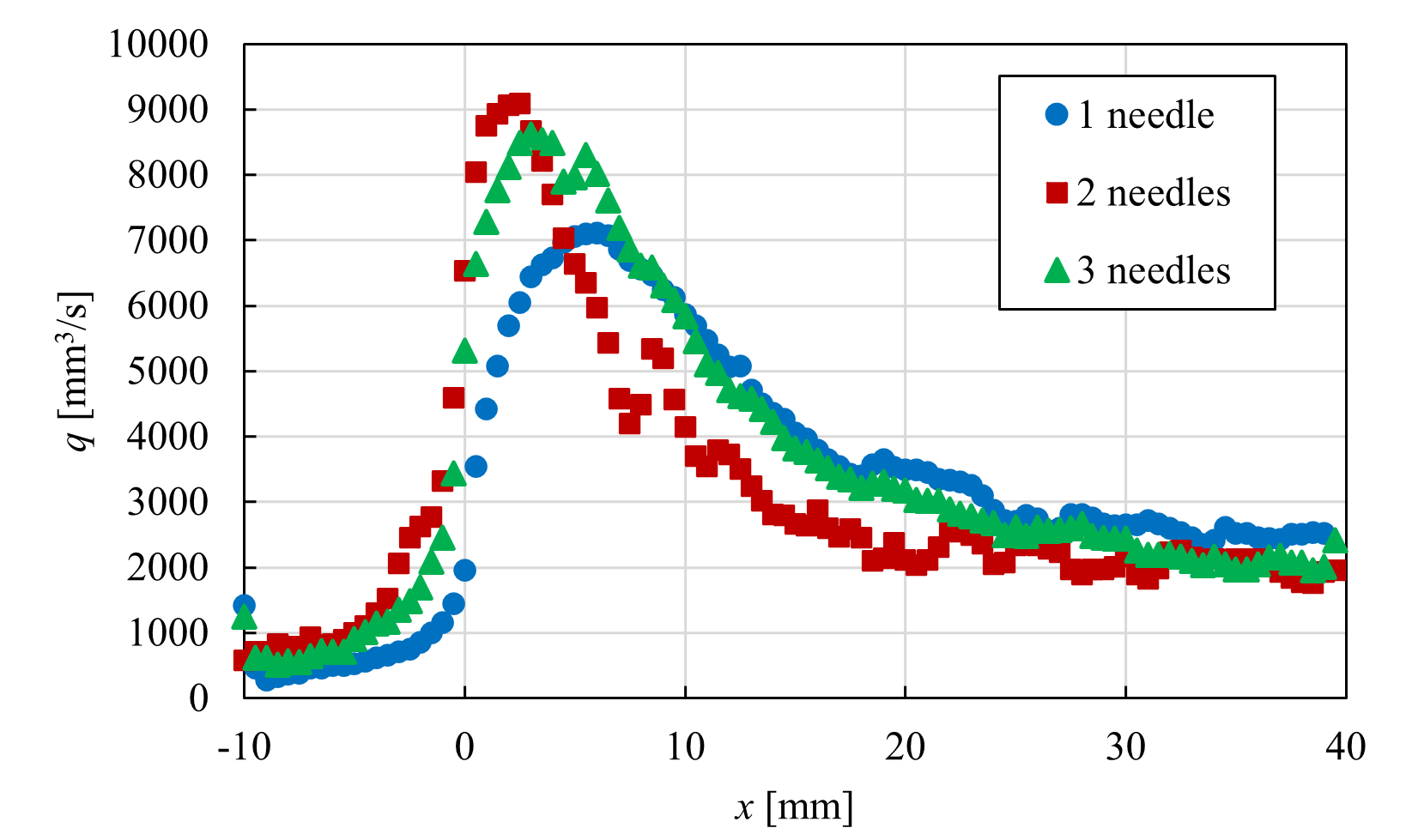． (a) z = 0 mm 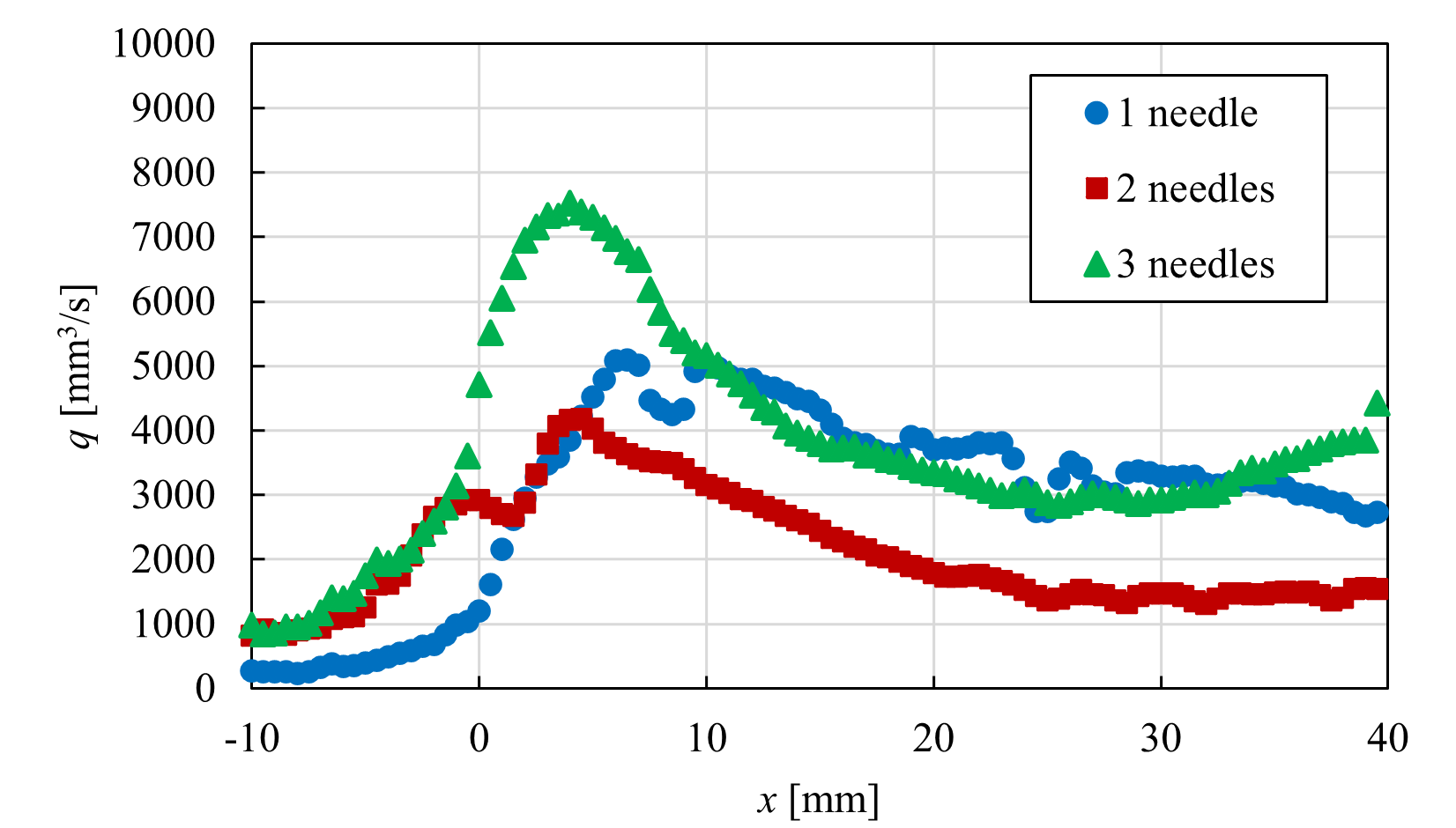(b) z = 2 mm 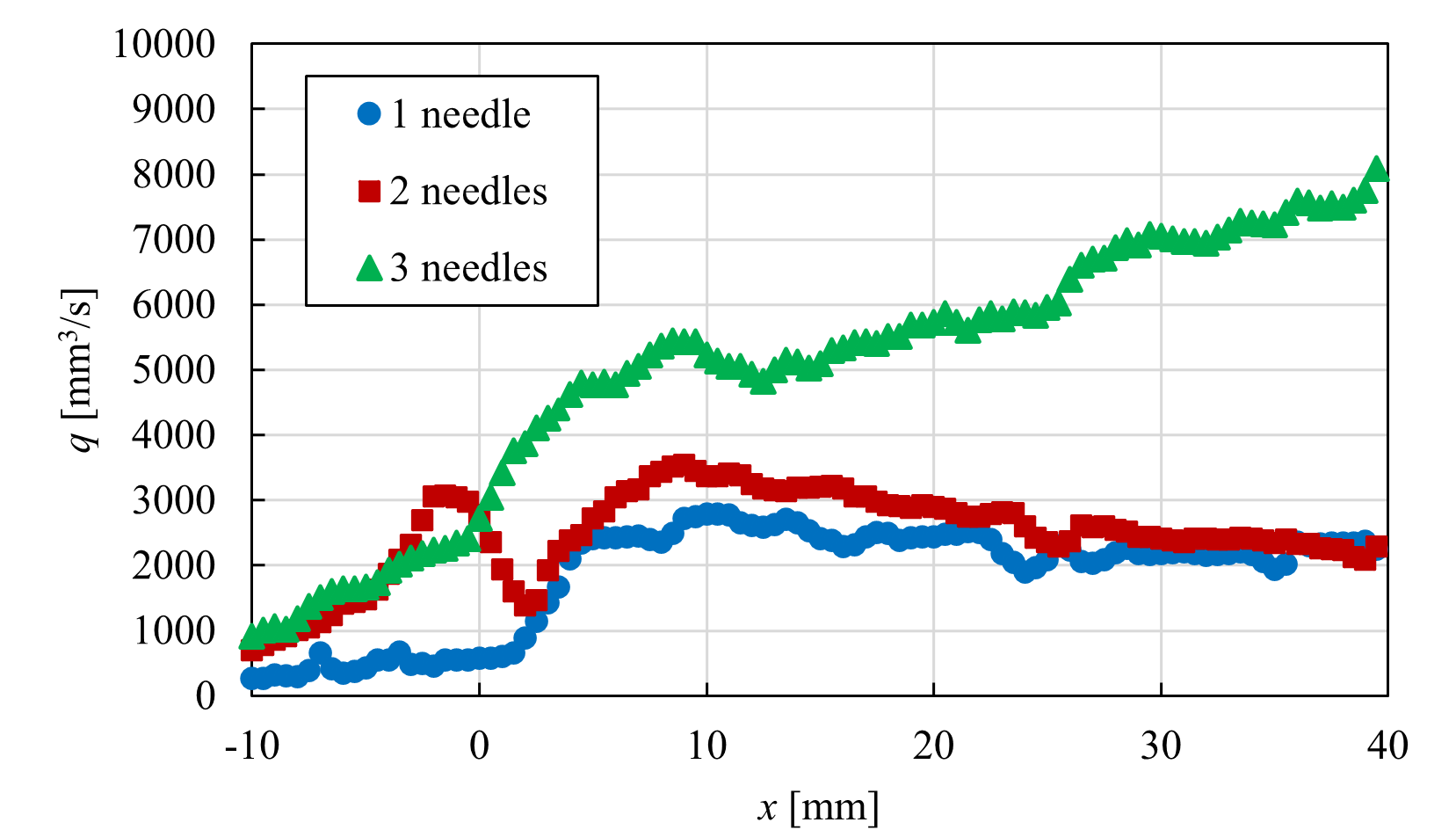(c) z = 4 mm Figure 7. 並列化前後での流量比較. <数値計算結果> 　針を3本用いて並列化した針型CD-PAにおいて，隣り合う針の間隔をw=10 mmとした場合の数値計算結果を，流速ベクトルとして図8に示す．ただし，片端の電極上をz=0 mm，両端の中心に位置する電極上をz=10 mm，もう一端の電極上をz=20 mmとし，表示断面は針電極間を2 mm間隔ごととした．また，電離した空気の電気伝導度σのパラメータa,bをそれぞれa=1.7,b=3.0としたときの結果を示している． 　図8より，両端の針電極の中心に位置する電極上での流速が大きくなっている．これは，中心に位置する針電極から誘起される流れと，両端の針電極から誘起されるそれぞれの流れの相乗効果が得られたためであると考えられる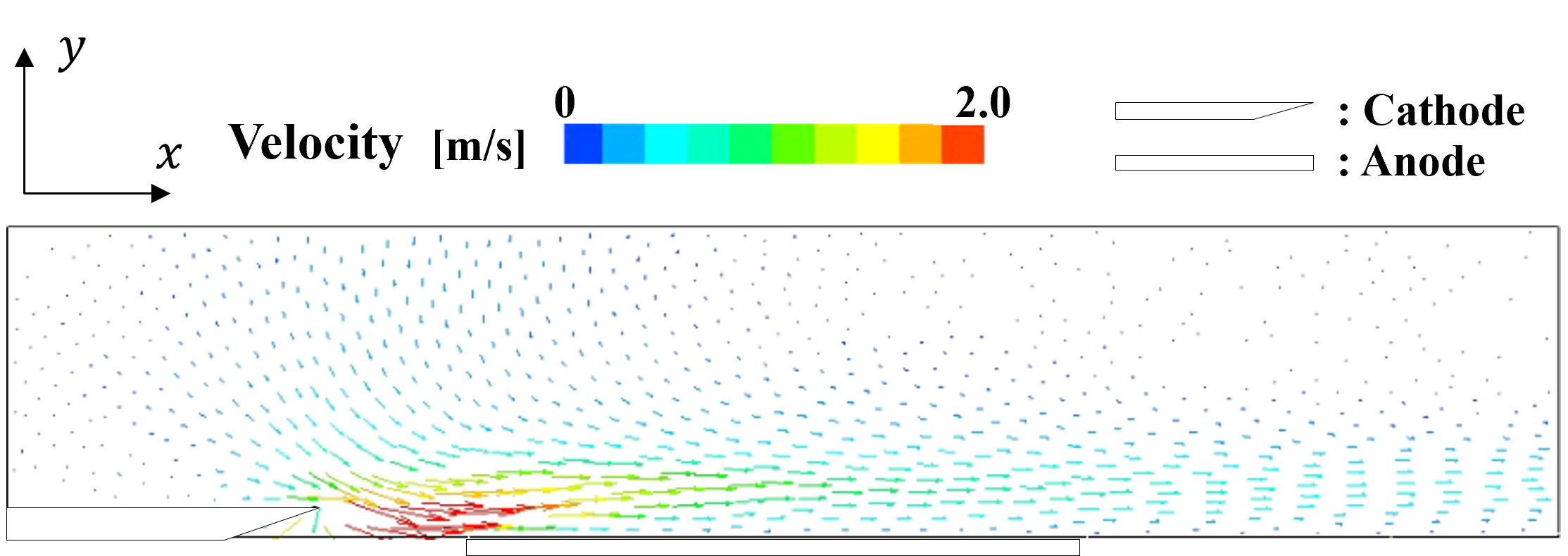． (a) z = 0 mm 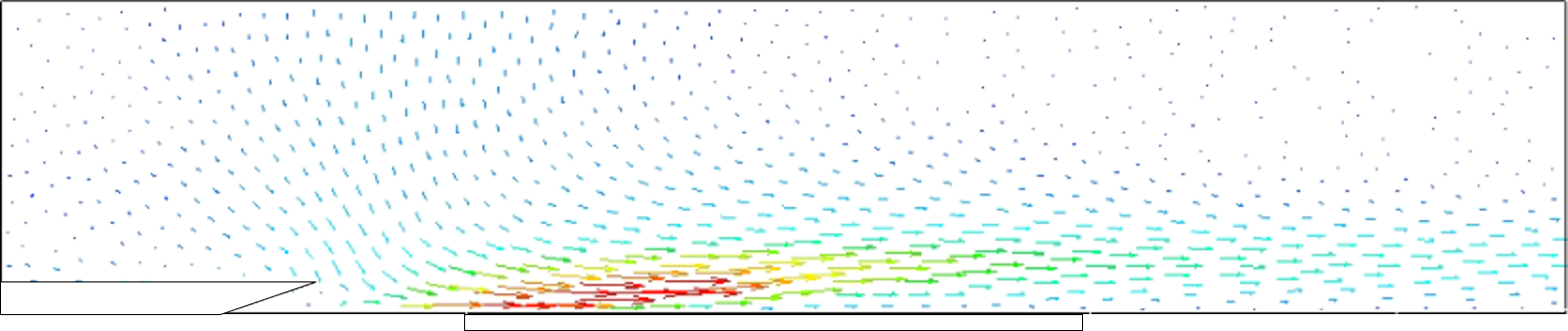(b) z = 2 mm 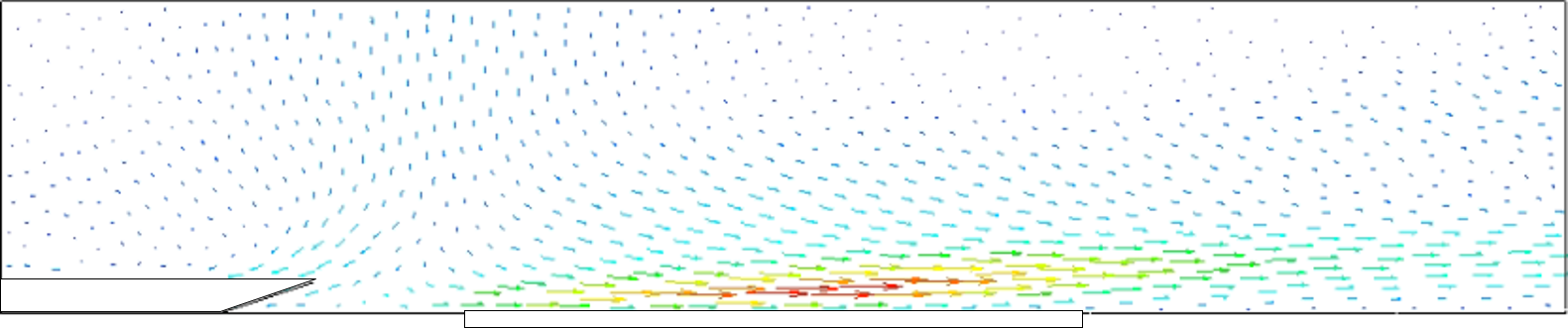(c) z = 4 mm (d) z = 6 mm (e) z = 8 mm 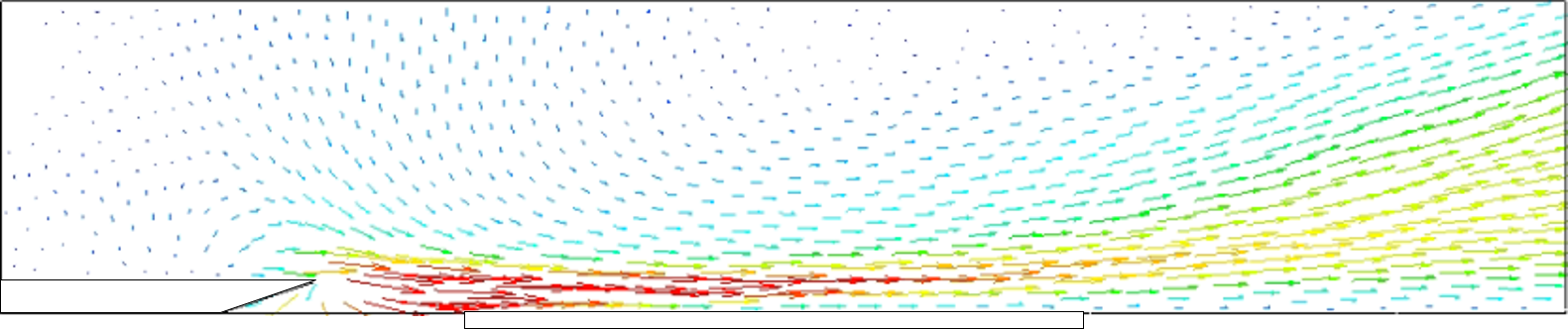(f) z = 10 mm Figure 8. 針を3本用いた場合の数値計算結果. 　次に，w=10 mmとした場合の各x方向位置における，実験結果と数値計算結果の主流方向流速プロファイルの比較を図9に示す．ここでは，針電極の先端をx = 0 mmとし，x = 5, 15, 25 mmの位置での結果を代表的なz=0,4,10 mmの場合について示す．ただし，PIVを用いて求めた流速は0.1秒間の時間平均である． 　図9より，すべての位置において，針電極上及び針電極間ともに定量的な一致が見られる． 　以上の結果から，数値計算で用いた本モデルは，w=10 mmの場合において，実験結果と比べて妥当なものであることが示された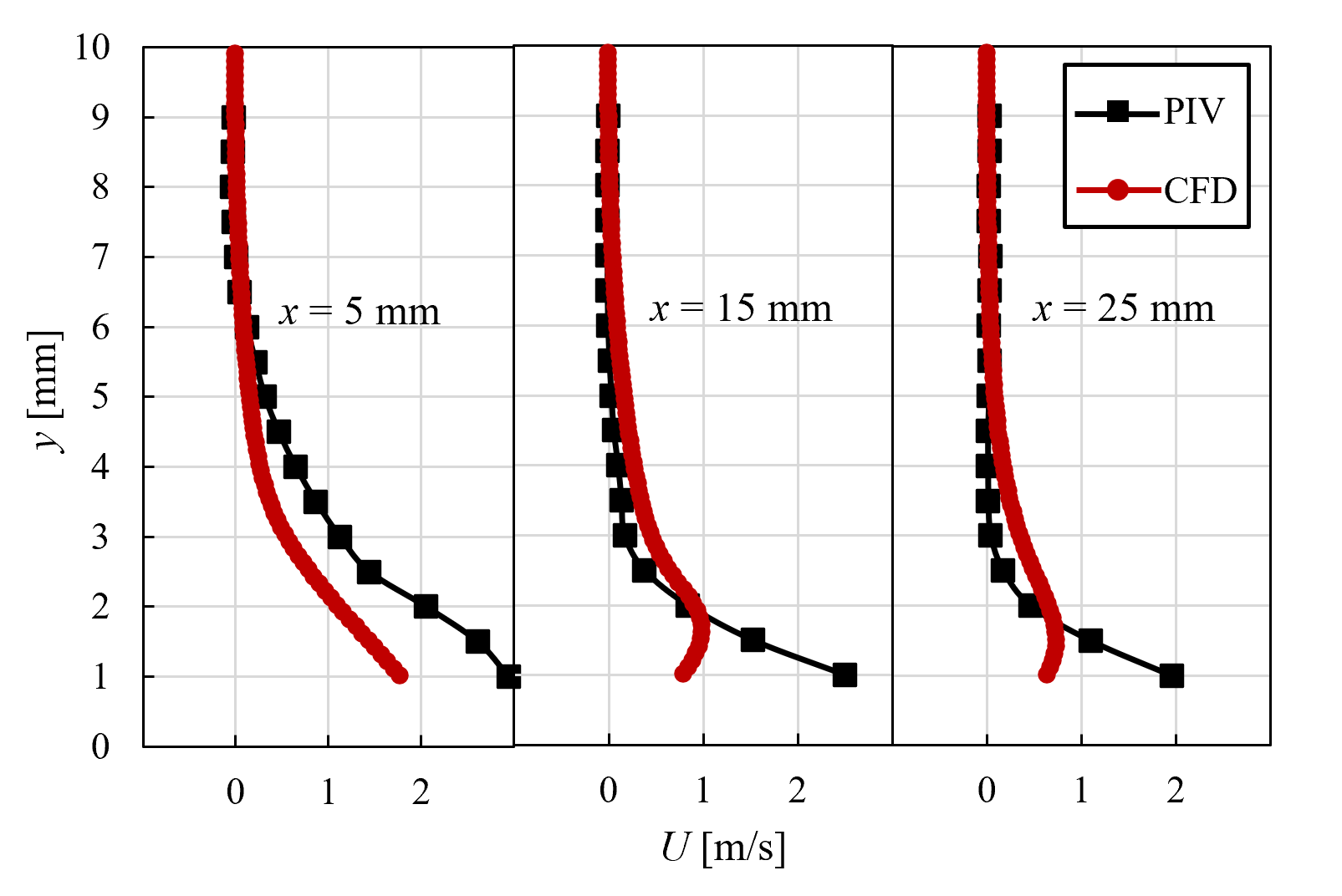． (a) z = 0 mm 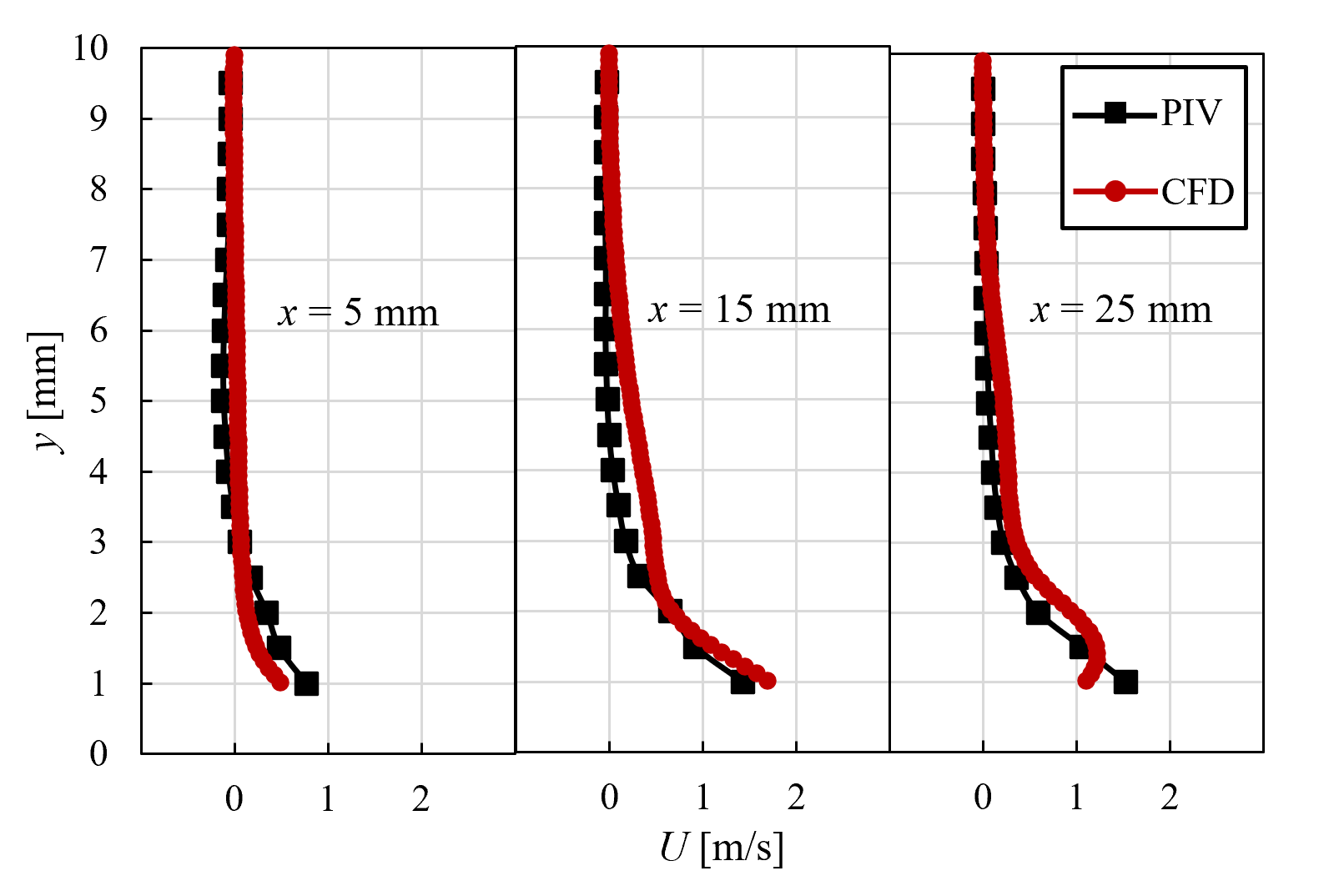(b) z = 4 mm 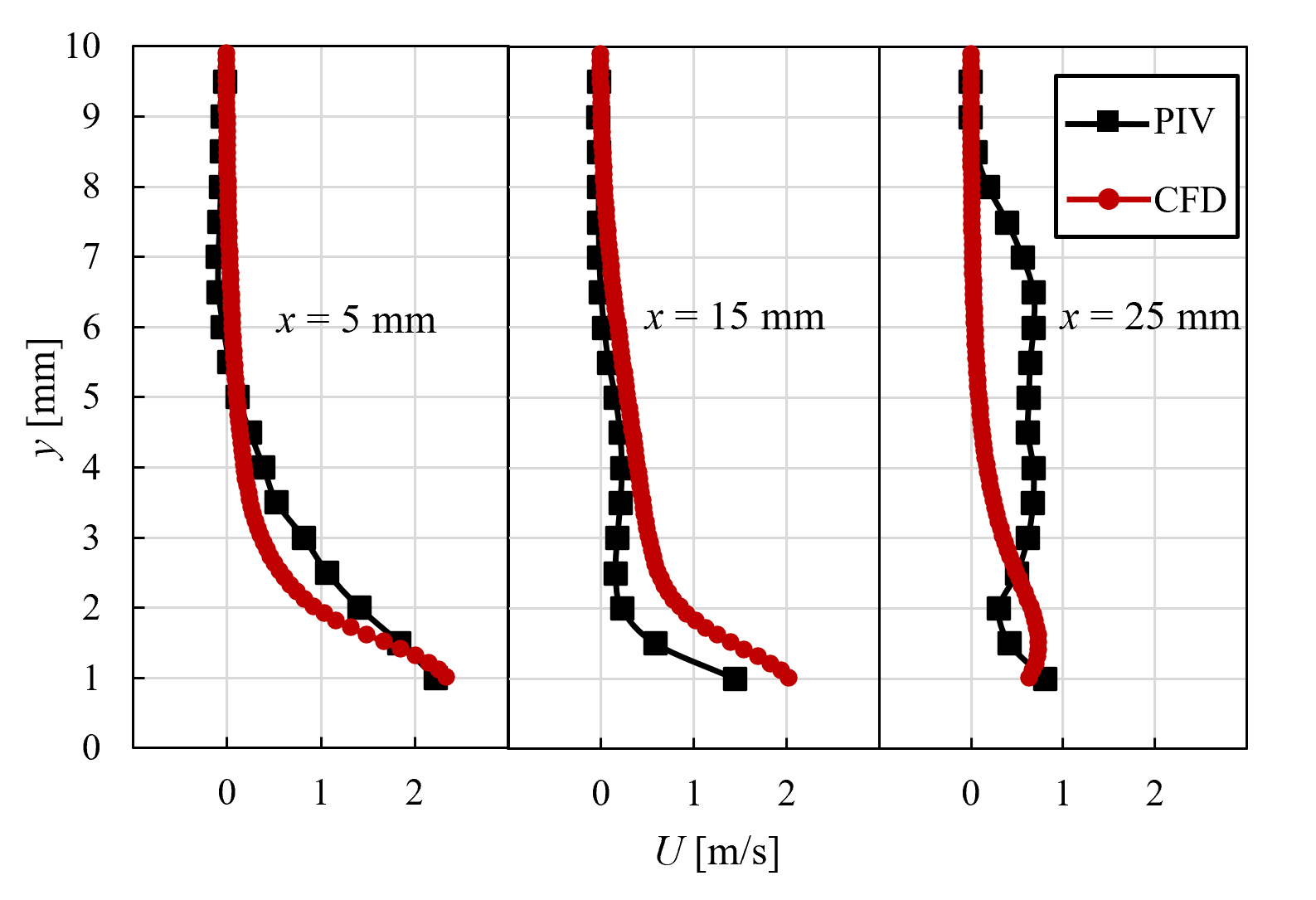(c) z = 10 mm Figure 9. 実験と数値計算の流速比較.