課題 新型環状プロペラの性能と騒音評価に関する研究 背景 　 　近年, 無人航空機 (Unmanned Aerial Vehicle: UAV), 通称ドローンの利用が官民問わず様々な用途で世界中に広がっている.その用途は,農薬の散布や架線の工事,荷物の輸送, 偵査, 戦術爆撃など多様である.ドローンの推進器はプロペラであるため，プロペラの性能はドローンの空力性能や騒音に直結する．空中物流や空飛ぶクルマの登場によって,将来は多数のドローンが都市上空を飛行することになるため，プロペラの騒音は都市部で騒音問題を引き起こす.そのため,プロペラから発生する騒音を低減する必要がある.ドローンが発する騒音の中で最も大きいものは，プロペラが風を切る際に生じる騒音であり,この風切音を小さくすることがそのままドローンの低騒音化に貢献する．特に回転翼機ではほとんどの場合，複数のプロペラを高速で回すことになるため，非常大きな騒音が発生する.これまでの研究で,翼形状が空力性能及び騒音へ及ぼす影響が調査されてきた． Figure 1. 空中交通（国土交通省）. 近年，MITリンカーン研究所は環形プロペラには低騒音,高効率の特性があると発表した.同年,JAXAは独自技術の低騒音プロペラ「Looprop」の静音効果を実証した.Sharrow Marine社は船用環形プロペラの商業化を実現したが,ドローン用環形プロペラは現在研究中である． Figure 2. ドローン環状プロペラ Figure 3. 船用環状プロペラ. 目的 本研究では，高効率かつ低騒音な新型の環状プロペラを研究するため，一般的なプロペラを基づいて，CFDによる数値解析と実験を行った．本発表では，プロペラは静止流体中に一定の回転数で設置され，環状プロペラ(L2)に加えて一般的な2枚羽根プロペラ(B2)と4枚羽根プロペラ(B4)を比較対象として，空力性能と騒音を評価した．モデルは図３で示す、左からそれぞれB2,B4,L2である。各断面無次元弦長と取り付け角度は図４で示す。 Figure 4. プロペラモデル. 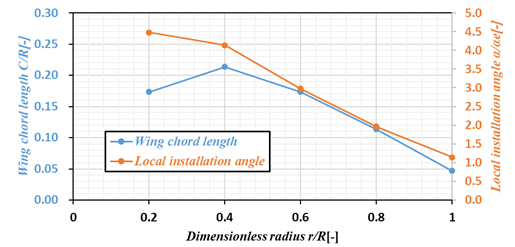Figure 5. 各断面無次元弦長と取り付け角度. 方法 本研究に使用した計算格子はANSYS Workbench 2023 R1を用いて作成した．図3で示したプロペラ直径を代表長さRとして，計算領域として直径1.2Rの円球状の回転領域を設けた．回転領域の外側に直径12Rの円球状の自由空間を用意し，その境界条件を全て大気圧解放とし，プロペラを滑りなし壁面とした．プロペラの固定回転数は50Hzを計算した．計算ポイントはハブから2Rに設定する．プロペラ周りの流れ場の検証を行うために自由空間用の計算格子に約 503万点， プロペラ周りの計算格子に約 211 万点を設け，総格子点数を約714万点とした．最少格子幅はプロペラ壁面の0.8 mmとした．計算には商用計算ソフト ANSYS CFX 2023 R1 を使用し，乱流モデルにはLESを使用し，計算を行った．時間刻みをΔt=5×10^(-5)とした． 翼通過周波数成分の騒音を除けば，翼面近傍の格子解像度上げることによって広帯域騒音の特性をある程度捕らえることが可能であることが示されている． 流体騒音源に関し，定格回転数(f=50Hz)における風速の最大値となる翼回転速度はVmax=2πRf[m⁄s] となる．このとき，翼外径を基準としたレイノルズ数は 4.2×10^5，マッハ数は Vmax/c となる．このため，流体騒音源は，二重極音源が支配的となる．そこで，計算ポイントの圧力変動に着目し，LESを用いた乱流による圧力変動の推定を行った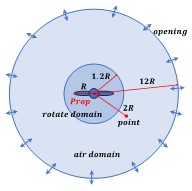． Figure 6. 数値計算領域. 　実験装置の概略図を図7に示す．実験で使用するモータCy-Captain 社製，CR23) はブラシレスモータである．プロペラモデルは図4で示して，3DプリンタでPLA樹脂を用いて製作したものを使用する．直流安定化電源(CUSTOM 社製， DPS-3003)から送られた一定電圧をサーボテスター (NOVATECH 社製，N-B608)を用いて，ESC (Hacker Motor GmbH 社製，X-12Pro)に信号を送り，モータの回転数制御を行った．騒音計(リオン社制，NL-42)とマイクを使って，サンプル周波数を20000 Hzとして10秒録音に取り込んだ．プロペラを50rpsの回転数で回転させる．半径方向無次元距離r/R=2を測定点とした．図7に赤×で示す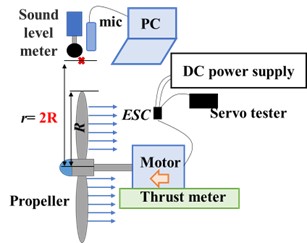． Figure 7. 実験装置. 結果 図8で示す静止性能指数のうち，L2が一番高い，0.6となる．次にB4が0.52で，B2が0.5と減少することが確認された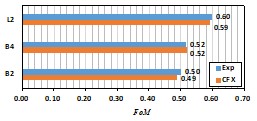． Figure 8. 静止性能指数. B2，B4，L2のブレード周りの渦は図9で示す，B2，L2のブレード先端渦が2つ，B4のブレード先端渦が4つ確認された． Figure 9. B2，B4，L2のブレード周りの渦. 図10はそれぞれB2，B4，L2の瞬時音圧レベルであり、時間により変わっているので、式(4)，(5)により時効音圧レベルに計算して、結果は図10で示す。B2，B4，L2の音圧レベルの実験とCFD結果を図10で示す，青色は実験結果，赤色はCFD結果である．全体的に，実験結果とCFD結果の差が４％以内になるので，定性的に一致する．図9により，B4の音圧レベルが一番小さく，平均的に78.9dBになる．次に，B2が平均83.7dBになる，L2が一番大きく，平均86.2dBになる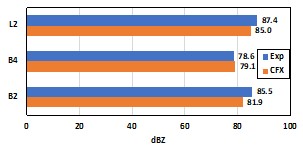． Figure 10. B2，B4，L2の瞬時音圧レベル.