課題 飛行機翼に生じる流体振動の解析と制御に関する研究 背景 フラッタとは橋や飛行機の翼などが気流のエネルギーを受けて起こす破壊的な振動を指す。図1のように翼が流れ場に置かれたとき、 翼近傍の空気の流れが変化し、それに伴い流体力が変化する。 変化する流体力は翼に振動を与えその振動がさらに翼近傍の空気の流れを変化させるというループができる。 これがいわゆる自励振動といわれるものである。 それらの振動は最悪の場合、図2のような翼の破壊を引き起こす危険性が考えられる。 現状の飛行機ではフラッタが発生しないように設計されているが、 将来、図3のような超音速機などの開発で空力的な要求から非常に薄い翼の設計が必要となると このフラッタ問題は極めて重要な課題になることが予想される。 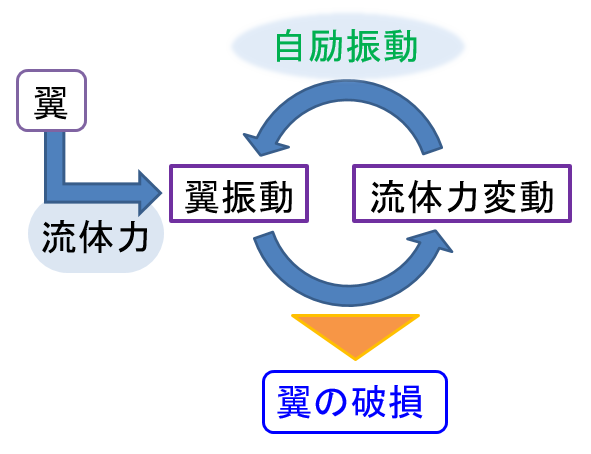　　 図1. フラッタの仕組み. 図2. フラッタの事故. 図3. 将来の機体. ※ＪＡＸＡより 目的 本研究では、翼が発生させるフラッタ振動を「並進振動」と「回転振動」に分離し、これらの振動を数学的に解析することによってフラッタ振動を解析することを目的としている。 また、振動解析を行うにあたり、特定の翼に対して実験と数値計算によって整合性を確かめる。 図4、図5にはそれぞれ一例としてNACA0012翼型を用いた実験と数値計算の様子を示している。 図4. 実験によるフラッタ振動の様子. 図5. 数値計算によるフラッタ振動（強制振動）の様子. 先行 研究 地上に静止している翼に各欄を与えても誘起された振動は時間とともに減衰するが（これを正減衰という）、翼が受ける空気の流れが速くなると、空気力は負減衰となり、振動が発生する。 正減衰と負減衰との境目に減衰力が0となり、調和振動を持続する点があり、この点をフラッタ限界という。 J.H.Greidanusは1949年にフラッタ方程式から非圧縮非粘性下での流体が平板翼に与える仕事を導出し、この仕事からエネルギー収支が0となるフラッタ限界を示したグラフを作成した。 図6には実際にGreidausが作成したグラフを示している。 ここで、このグラフは角周波数を無次元化した無次元周波数をパラメータとして作成されている。 このグラフは、曲線状の点がフラッタ限界、曲線外が正減衰、曲線内が負減衰であることを表している。 つまりこの理論を理解することは、翼の振動を制御するためには、非常に重要となる。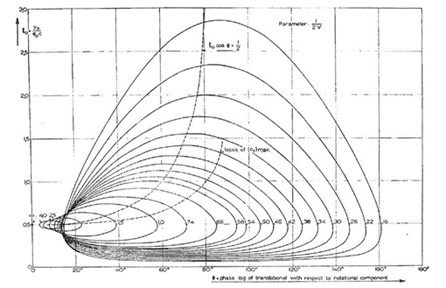 図6. J.H.Greidanusのフラッタ限界のグラフ. 理論 図6は、J.H.Greidanusが1949年に発表したものであり、具体的な計算過程や数値が残っていない。 そこで、このグラフを作成する計算過程を簡単に記載する。 ここでは、図7のような2自由度のフラッタモデルについて考える。 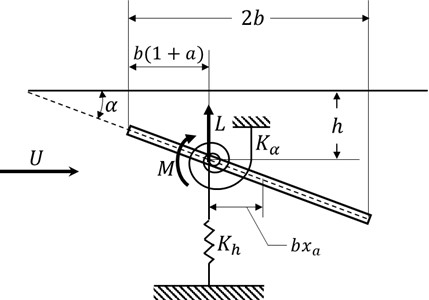図7. 平板翼におけるフラッタモデル. 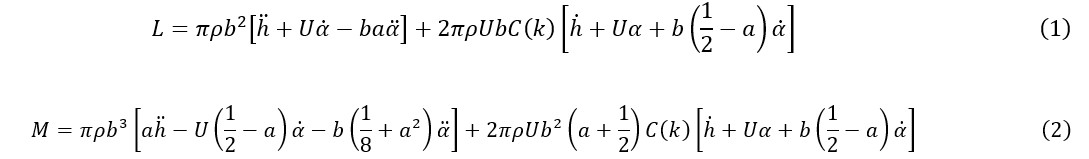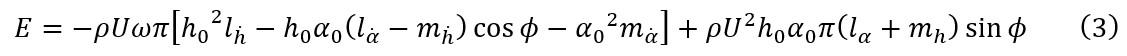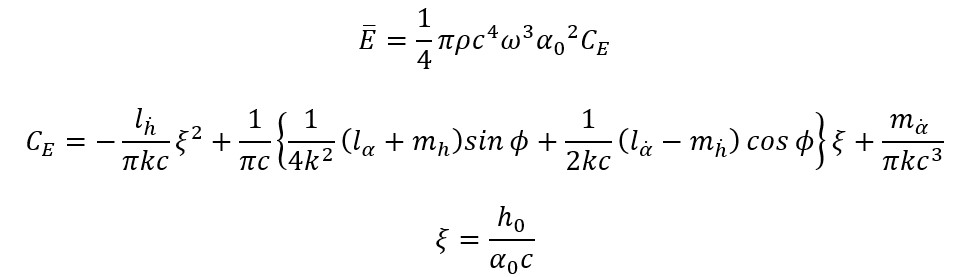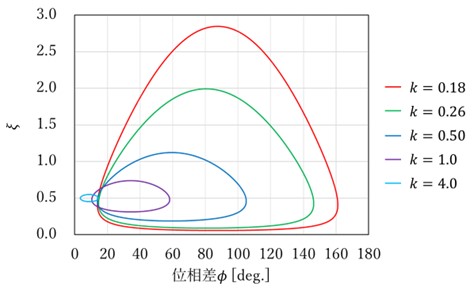非定常空気力学の示すとことによると、振動数$ω$で調和的に並進振動$h$と、前縁から$b(1+a)$の点まわりの回転振動$α$を行う二次元平板翼に作用する空気力は式(1)、(2)のように表すことができる. ここで，$L$は揚力、$M$はピッチ軸周りのモーメト、$k$は無次元周波数、$C(k)=F(k)+iG(k)$はTheodorsen関数である。 式(1)、(2)より、MCK型の二次元平板翼のフラッタ方程式を作成できる。 この方程式を解くことによって、式(3)に示すような振動1周期の翼が空気に与える仕事$E$を算出することができる。 Greadanusはこれを整理し、仕事$E$を1周期で割った平均仕事$\bar{E}$から以下のような係数$C_E$を求め、$C_E=0$となる時の$ξ$と位相差$ϕ$の関係を示した。 図8に、この式より作成したフラッタ限界のグラフを示している。これは、図6に示したGreadanusのグラフに一致していることが分かる。 このグラフを活用して数値計算・実験を行うことで、理論的にフラッタを解釈できるようになる。 図8. 各無次元周波数ごとのフラッタ限界.