課題 翼列流れに関する研究 背景 　フラッタとは橋や飛行機の翼などが気流のエネルギーを受けて起こす破壊的な振動を指す。図1のように翼が流れ場に置かれたとき、 翼近傍の空気の流れが変化し、それに伴い流体力が変化する。 変化する流体力は翼に振動を与えその振動がさらに翼近傍の空気の流れを変化させるというループができる。 これがいわゆる自励振動といわれるものである。 それらの振動は最悪の場合、翼の破壊を引き起こす。 　タービンとは，ガスタービンの構成要素の一つであり，多くの翼がケーシングに固定されている静翼列(Stator)と，翼がタービンディスクに植え込まれている動翼列(Rotor)からなる段で構成されている．燃焼器で発した高温高圧ガスが亜音速から超音速でタービンを通過するときに，静翼列で整流された流れが動翼列に仕事を与えることで回転力を得ている． 　圧縮機やタービンのように多数の翼が並んでいる状態で生じるフラッタのことを翼列フラッタという。ある翼が何かしらの原因で振動を始めると，その振動によって誘起される空気力が隣の翼に影響を与える。このような相互干渉は隣り合う翼同士だけでなく，同じ翼列内のさらに遠くの翼との間にも存在する．この相互干渉によって条件によっては翼列フラッタが生じる．このフラッタの影響によって，翼のみでなく流体機械そのものに影響を及ぼす可能性がある．そのため，翼列フラッタの抑制は非常に重要となる． 　2022年、宇宙航空研究開発機構（JAXA）ではH3ロケットにおけるLE-9エンジンの開発が進められている．その中で，エンジン内部のタービンで翼列フラッタの発生が確認され，実際に問題となっている．図２にタービン翼列フラッタの例を示す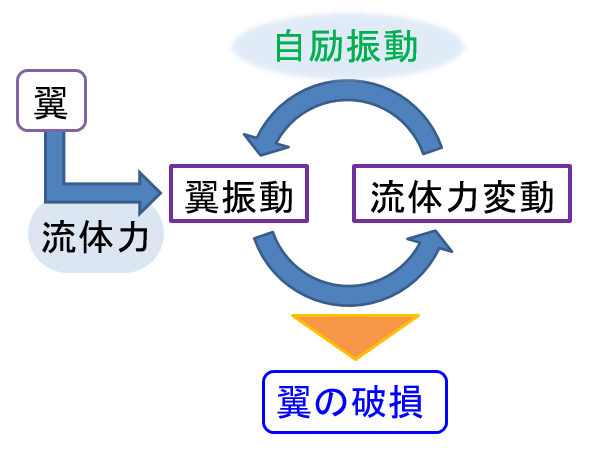． Figure 1. フラッタの仕組み. 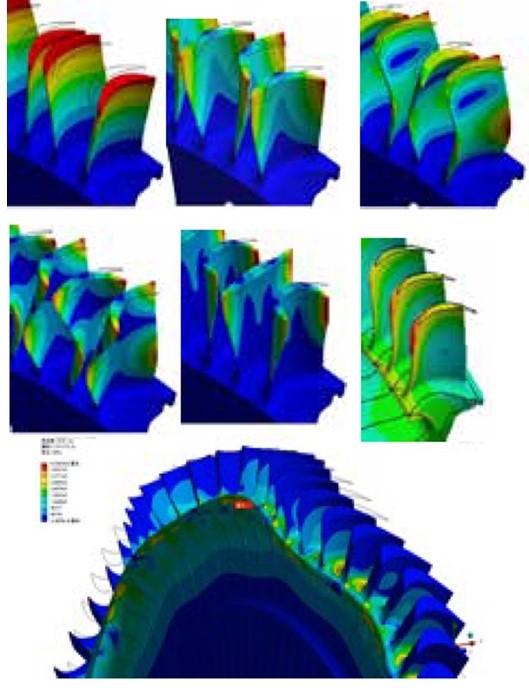Figure 2. タービン翼列のフラッタ. ※参考文献：岡田匡史，H3ロケット第1段エンジン(LE-9)の開発状況について(2022),p7,宇宙航空研究開発機構 目的 　前節でも述べたように，タービン翼列フラッタは実際にジェットエンジン内部でも発生し問題となっている．よってタービン翼列フラッタに関する研究が長く続けられている．そこで今回，タービン翼列フラッタ発生に関わる，タービン翼列流れに関する研究を行った．本研究では，翼列における流れ場や衝撃波の検証を目的とし，翼列流れの三次元非定常数値解析を行った． 方法 　数値計算を行うためには、まず図3のような計算格子を作成する必要がある。この格子は、計算格子作成ソフトPointwise V17.1R4を用いて作成した。また、数値計算ソフトはANSYS CFX 2022 R2を使用する。ANSYS CFXでPointwiseによって作成した格子を展開して実際に数値計算を行う。 　数値計算で用いた静翼と動翼は二次曲線と円弧を組み合わせて設計した。動翼列に187rad/sの周速を与えた状態で3次元の非定常数値計算を行った。支配方程式は圧縮性ナビエストークス方程式、乱流モデルはk-イプシロンとした。格子点数は約390万点とした。また、翼列を再現するために本数値計算では計算領域の上下の境界を周期境界に設定した。なお周期境界とは、境界の上下をつなげ計算領域を円周上に連続させる条件のことである。数値計算の境界条件としては入口全圧を４気圧、出口静圧を0.1気圧に設定し、入口から出口に向かって空気が流れるようにした。 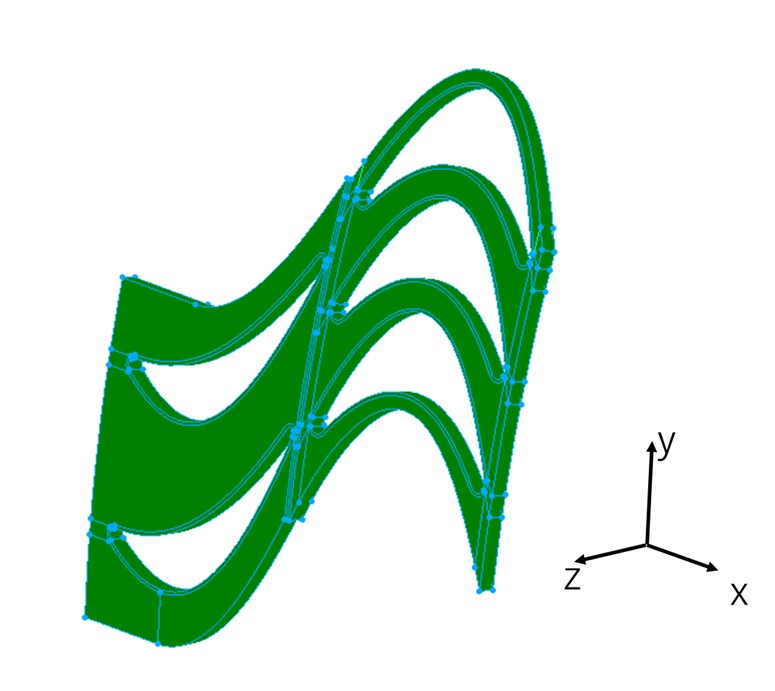　 Figure 3. 動翼周りの計算格子. 結果 　本節では，非定常数値計算で得られた翼列における圧力分布とマッハ数分布を示す．ここでは，スパン中心面の流れ場の様子を示す．非定常計算において，流れの状態変動が周期的になって，さらに計算を開始したときと翼列の配置が同じになったある瞬間を t = 0 s とし，一枚の動翼が一静翼間を通過するまでの時間を周期 T として，T/4 ごとの流れ場の圧力分布，マッハ数分布をそれぞれ図 4，図 5 に示す．なお，周期境界条件による計算結果を見やすくするために，図 4 と図 5 では，静動翼列を上下に連続させて表示している．また，以下言及しやすくするために，各静翼をそれぞれ(1)，(2)，各動翼をそれぞれ(I)，(II)，(III)と名付けることとする．動翼列入口，動翼列中央それぞれに設置した観測点のマッハ数変動の様子を図 6 に示す． 　図 4 より，入口上流から出口下流に向かって圧力が徐々に減少することが分かった．静翼前縁付近の圧力はほぼ 4 atmであるが，静翼後縁付近では 3 atm.に近くなっており，動翼列入口付近から圧力が急激に下がることが分かった．動翼を通過するにつれて圧力は減少し 0.1 atm.付近となった．特に，動翼列スロート付近での圧力勾配は，他の場所と比べて大きく，圧力が低下することが分かった． 　図 5 より，入口上流から出口下流に向かってマッハ数が徐々に上昇することが分かった．静翼前縁付近のマッハ数はほぼ 0 であるが，静翼後縁付近ではおよそ0.5 となっており，動翼列入口付近から流れがさらに加速されていることが分かった．これは動翼列入口で流れが絞られているからだと考えられる．その後，動翼列を通過するにつれて，流れはスロートに達し，マッハ数は上昇し 1 付近となった．動翼列出口付近では，マッハ数がさらに上昇し，1.4 以上まで加速した．これは，動翼列がラバルノズルの作用をしたため，流れが超音速まで加速されたのだと考えられる． 　図 6 左縦軸，右縦軸に動翼列入口，動翼列中央それぞれのマッハ数変動を示す．非定常計算において，流れの状態変動が周期的になって，さらに計算を開始したときと翼列の配置が同じになったある瞬間を t = 0 s としている．なお横軸の t*は一静翼間を一枚の動翼が通過する時間周期を T として，経過時間 t を T で割って無次元化したものである．このグラフから，動翼列入口のマッハ数は振幅が約 0.05，周期が 1t*で周期的に変動していることが分かる． また，動翼列中央のマッハ数は振幅が約 0.04，周期が 1t*で周期的に変動していることが分かる．これら 2 つの点におけるマッハ数が 1t*の周期で振動していることから，このマッハ数変動は動翼によって引き起こされていると考えられる．流れ場で流体振動が起こっていることから，翼に何らかの振動を与える可能性が考えられる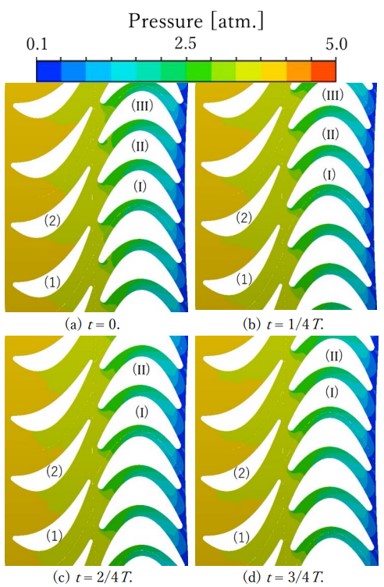． Figure 4. 圧力分布. 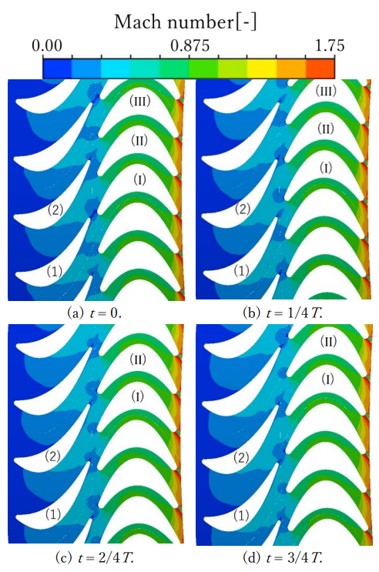Figure 5. マッハ数分布. 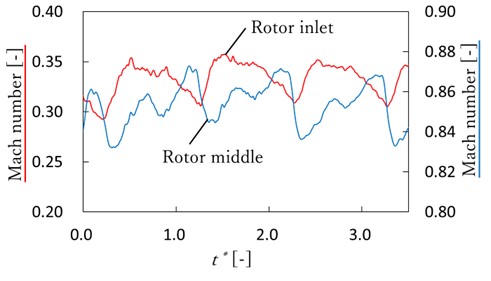Figure 6. マッハ数変動.