課題 円柱のアスペクト比と流体振動の関係程 背景 　送電線，斜張橋，及び海底ケーブルなどにおいて，風や海流によるケーブルのフラッタやギャロッピングが問題となる．直径に対する長さの比（以下アスペクト比）が異なると振動も異なることがよく知られている． また，雨や雪，ごみの付着により，ケーブル断面が非真円で非対称となり，空力振動現象も複雑化する. 　このような流れ場中に置かれた構造物の振動特性について知見を得ることは，非常に有用である． Figure 1. 斜張橋. 目的 　本研究では，様々なアスペクト比を持つ物体の空力振動と物体周囲の流れの変動との関係を明らかにすることを目的とした． 先ず，径の異なる7つのチューブを流れに垂直に設置した場合における，流速の変動を調査した．また，得られた振動周期を先行研究のデータと比較することで，実験方法の妥当性を検証した． 続いて，チューブを流れに対し垂直に設置した場合のチューブの振動を調査し，流れの変動現象との比較を行った． 実験装置と方法 　図2に測定部の概略図を示す．測定部は600×600mmの正方断面で，全長は約3000mmである．送風機の十分下流に固定用具を設置し，チューブを設置する． チューブは，直径D=2, 4, 6, 8, 10, 16, 20mm（アスペクト比Ra=300, 150, 100, 75, 60, 37.5, 30）の7種類の円形断面を持つシリコンゴムチューブを用いた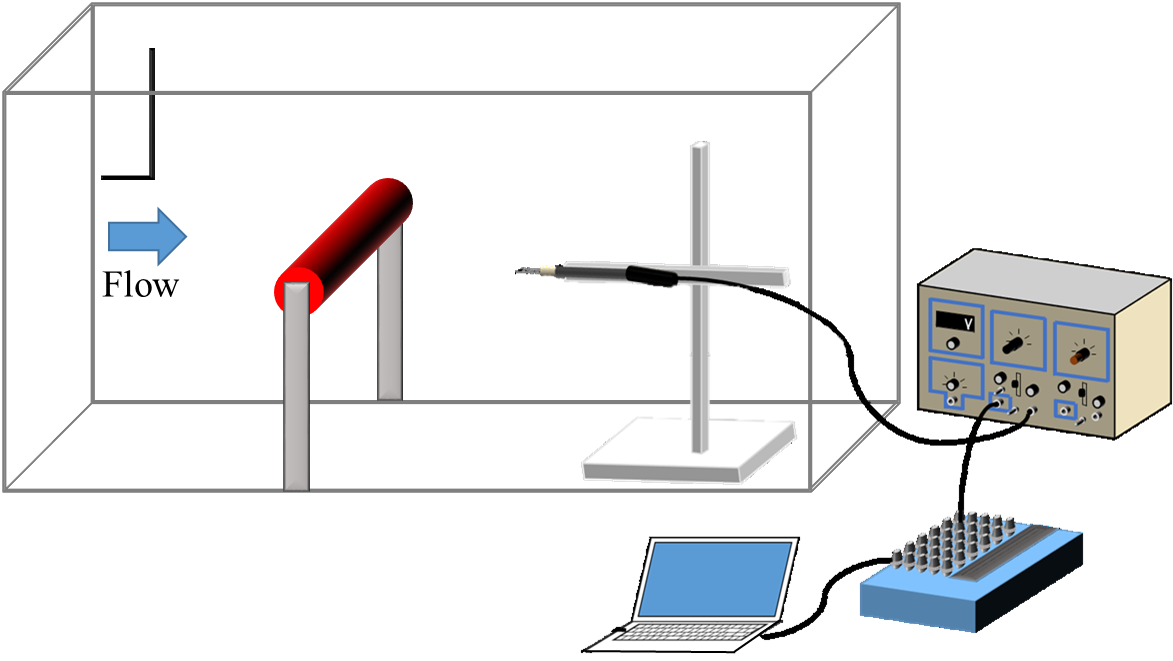． Figure 2. 実験装置. 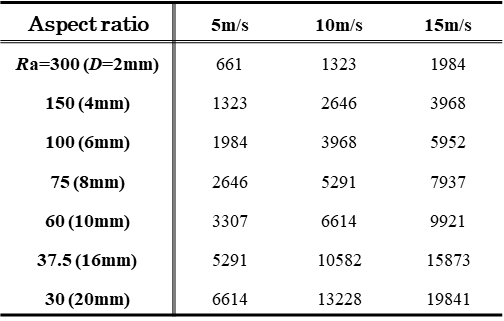　図2に示すように，チューブ下流の流速の変動を測定するため，I型熱線プローブおよび定温型流速計を用いて，電圧波形を取得した． プローブは，チューブの軸と同じ高さのスパン中央とし，チューブ円心より5D下流側に設置した．サンプル数を10240，サンプル周波数を1024 Hzとして10秒間計測した． 熱線流速計で得られた電圧波形を高速フーリエ変換（FFT）し，チューブ下流における流速の変動周波数を求めた． また，熱線プローブと同様の位置にハイスピードカメラを設置し，チューブスパン中央の振動の様子を撮影した． フレームレート1200とした．撮影した画像を二値化し，スパン中央における振動に対して高速フーリエ変換（FFT）し，チューブの振動周波数及び振幅を求めた． 主流の流速は，5m/s，10m/sと15m/sとした．各条件におけるレイノルズ数Re=UD/（Uは主流速度，は空気の動粘性係数）を，表1に示す． Table 1. 各流速およチューブ直径におけるレイノルズ数. 実験結果 熱線流速計による計測 　図3に，熱線流速計より得られた電圧変動をFFT解析した結果を示す．図3(a)は主流流速5m/s，図3(b)は主流流速10m/s，図3(c)は主流流速15m/sの場合の結果である． 横軸はストローハル数St（=fD/U，f：卓越周波数[Hz]，U：主流速度[m/s]）であり，縦軸は電圧である．熱線流速計で得られた電圧変動は，チューブ下流の流速変動を表している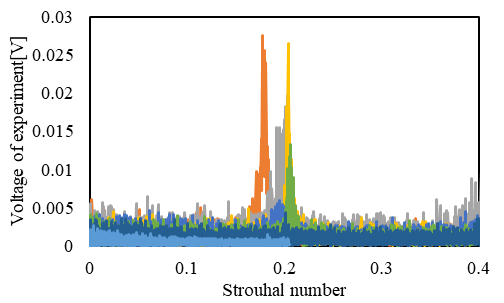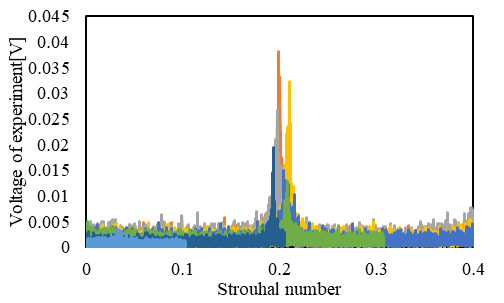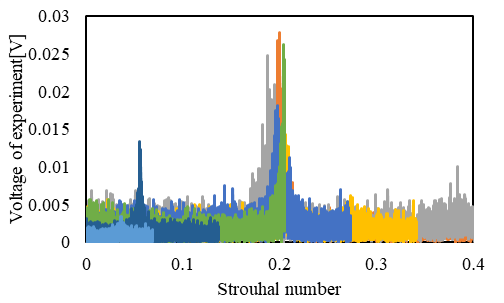． (a)　　　　　　　　　　　　　　　　(b)　　　　　　　　　　　　　　　(c) Figure 3. カルマン渦の放出周波数. 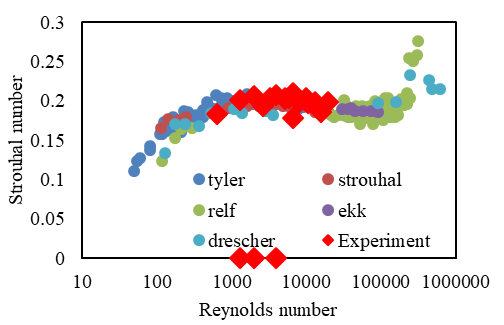　本実験では，チューブアスペクト比300及び150の条件において，流速変動計測の時間分解能が不足していたため，スペクトルピークが確認できなかった． 一方，それ以外の条件では，チューブの径や主流流速によらず，St =0.2付近で流速の変動はスペクトルピークをもつことがわかる． 図4に，各先行研究によるReに対する円柱周りの流れの変動周波数と，本実験により得られた結果を示している．横軸はRe，縦軸はStである． 円柱から放出されるカルマン渦の渦放出周波数は、レイノルズ数Reが500～2×105の範囲で，St = 0.2程度であること知られている．図4より，先行研究においても概ねSt=0.2であり，本実験でも概ね同程度の値をとなっていることがわかる． また，先行研究のStは，Reに対して3次関数的に変化しており，本実験の範囲でも，Reが小さくなるにつれてストローハル数も小さくなっており，同じ傾向を示していることがわかる．これより，本実験結果は妥当性があると考えられる． Figure 4. ストローハル数の比較. 高速カメラによる空力振動 　図5に，ハイスピードカメラで得られたチューブのスパン中央における中心位置の変位をFFT解析した結果を示す．主流流速が10m/sの結果である．横軸は，振幅変動の周波数であり，縦軸は振幅である． 図5より，アスペクト比によらず，約8Hzと100Hzでスペクトルピークが2つ見られることがわかる．8Hzのスペクトルピークでは，チューブのアスペクト比が小さいほど振幅が大きい傾向を示している． 100Hzの振動振幅は，8Hzの振動に比べてアスペクト比による違いは小さかった．また，主流流速が5m/s，及び15m/sの場合においても，8Hzと100Hzでスペクトルピークが見られた． 加えて，8Hzの振幅は，主流流速が大きいほど振幅も大きく，各条件において異なったが，100Hzの振幅は，すべての条件において0.6～1.0mmの範囲であった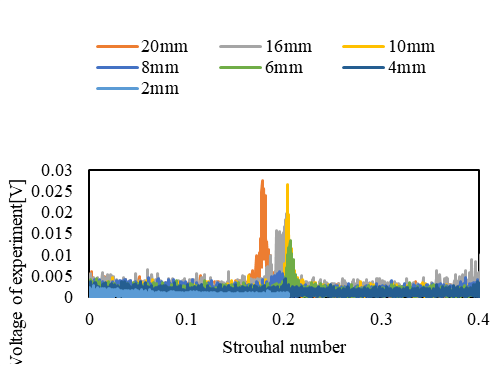． Figure 5. チューブの振動周波数. 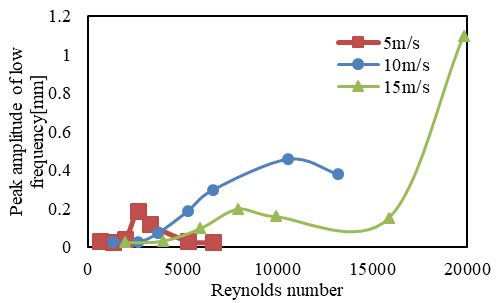　図6に，各流速における異なるアスペクト比のチューブの振動振幅を示す．横軸は無次元化したレイノルズ数Re，縦軸は低周波数側である8Hzのスペクトルピークにおける振幅である． 主流流速5m/sの場合，レイノルズ数Reの増加に伴い，振幅も増加して最大値を迎え，その後レイノルズ数の増加とともに振幅は小さくなる． 主流流速10m/sの場合も本実験の範囲では，同様の傾向を示し，レイノルズ数が約11000付近で振幅が最大となる． 一方で，15m/sの場合は，レイノルズ数が約8000で振幅が極大となり，その後レイノルズ数の増加とともに一旦は減少してレイノルズ数が約14000近傍で極小となる． さらに，レイノルズ数が増加すると，振幅も増加し，3次関数の変化を示した． Figure 6. 各レイノルズ数における最大振幅.