課題 絞り部に発生するキャビテーションの挙動に関する研究 背景 　キャビテーションサージは典型的な非定常現象であり, 油圧システムの騒音や振動の問題の原因となる. 流体機械内部において周期的な流量および圧力変動をもたらし，ポンプ脈動を生じさせる． 多くのCFD解析が行われているが，キャビテーション発生領域と周囲の配管系内の動特性との練成問題として解かなければならないため，計算に大幅な時間がかかってしまう． 能見らは非圧縮性二次元解析と，配管系の圧縮性を考慮した特性曲線法による練成解析手法を開発した. ・図1:キャビテーション ⇒液体の流れの中で, 圧力が飽和水蒸気圧よりも低くなった際に液体が常温で沸騰し, 泡の発生と消滅が繰り返す現象である. ・図2:CFD解析 ⇒流体の流れの運動に関する方程式をコンピュータで解くことによって流れを観察する数値解析・シミュレーション手法である. ・図3:キャビテーションサージ ⇒キャビテーションが発生しているポンプを含む流路系全体の不安定現象 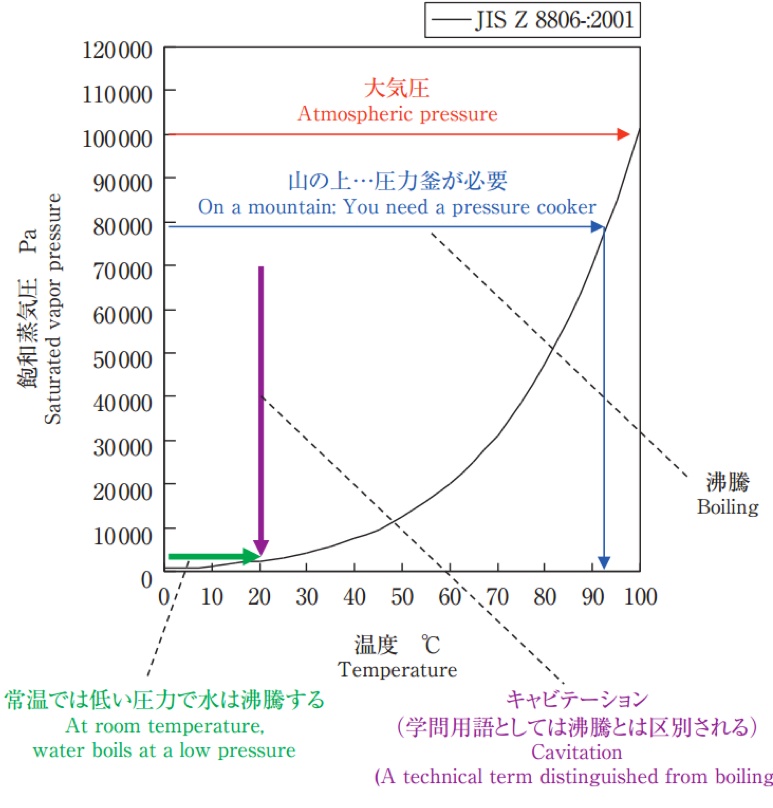図1. キャビテーション. 図2. CFD解析. 図3. キャビテーションサージ. 目的 　二次元絞り流路に着目し解析を行う． 能見らは非圧縮性二次元解析と，配管系の圧縮性を考慮した特性曲線法による練成解析手法を開発した. 1.絞り部のみ：二次元キャビテーション解析 2.絞り部と配管系：二次元キャビテーション解析 3.絞り部：二次元キャビテーション解析＋配管系:特製曲線法 ⇒しかし, いずれも絞り部上流へ圧力の変動が伝わらなかった. ・この研究では二次元絞り流路に注目して調査を行う. ・図4:実験に使用される配管系 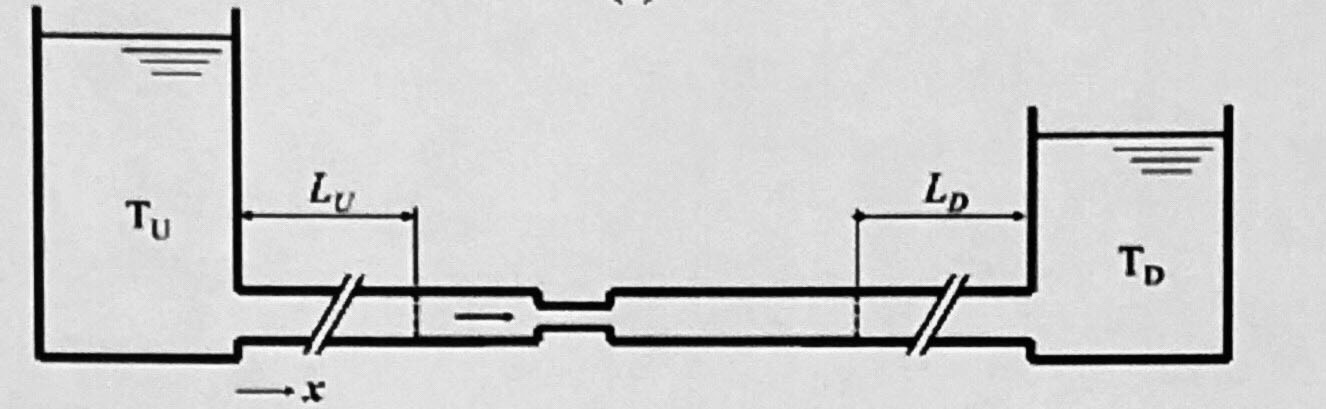図4. 配管系. 方法 ・計算ソフトウェア：商用ソフトウェアのANSYS Fluent19.2を使用． ・支配方程式：気相体積分率の輸送方程式, 非圧縮性Navier-Stokes方程式と連続の式. ・計算条件：乱流モデルがSST モデル, キャビテーションモデルがSchnerr-Sauer model, 壁面近傍には滑りなし条件. ・境界条件：入口速度を5m/s, 出口圧力は順次下げる, 非キャビテーション状態からキャビテーションの発生過程を観察. ・図5：実験に用いる二次元絞り流路. ・図6：6600セルの絞り部. ・図7:103000セルの絞り部. 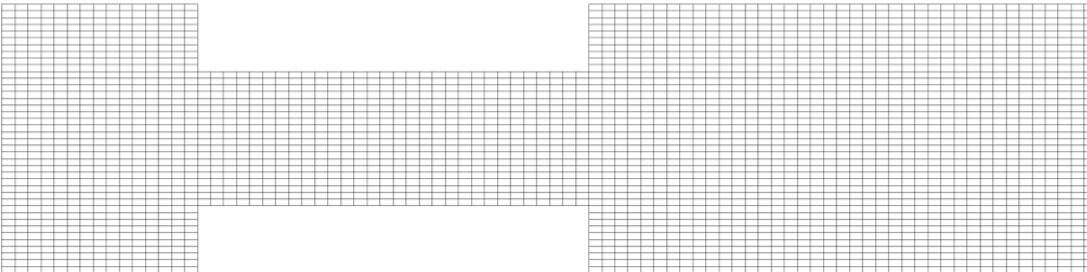図5. Nohmi et al, Cavitation CFD analyses considering the pressure wave propagation within the piping systems(2018) . 図6. 6600セル格子. 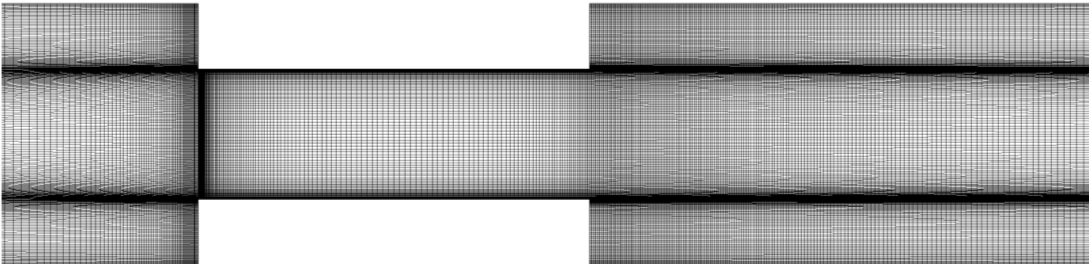図7. Title. 結果 　実験結果は以下の通りである． 1.絞り部後方の長さを２倍にした.(図8) ⇒出口境界では流速は一様に近づく. 2.格子を細かくする(図9). ⇒絞り部後方の非対称性は解消されない. 3.出口圧力を時間変動(図10). ⇒圧力が上流へ伝わらない時間が発生. 　飽和蒸気圧まで下がるとそれ以下に圧力が下がらなくなる. 図8. 絞り部後方の長さを２倍. 図9. 格子を細かくする. 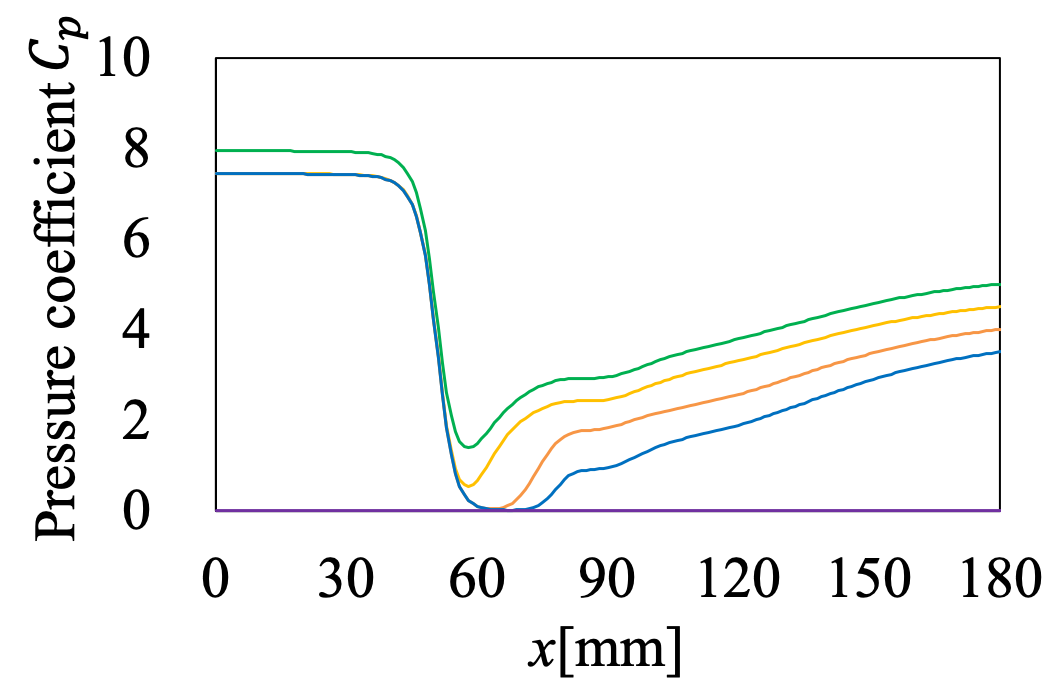図10. 出口圧力を時間変動.