| 課題 | 超音速ノズル内部において発生するはく離の抑制 | |||||||||
| 背景 |
ロケットノズルには円錐型,ベル型,プラグ型など様々な形状があり,現在最も多く用いられる形状は円錐型およびベル型である.
ノズル内部において、Free Shock Separation(FSS)と呼ばれる流れのはく離が生じる.
また,LE-7Aをはじめとするメインエンジンに用いられるCompressed Truncated Perfect(CTP)ノズルや,SSMEに用いられるThrust Optimized(TO)ノズルにおいて,
Restricted Shock Separation(RSS)と呼ばれる流れのはく離が生じる.それぞれのはく離の形態は以下のとおりである.
・FSS: ノズル内部においてはく離した流れが,はく離点下流で壁面に再付着することなく外部に流出する形態 ・RSS: ノズル内部においてはく離した流れが,はく離点下流で壁面に再付着してノズル外部に流出する形態 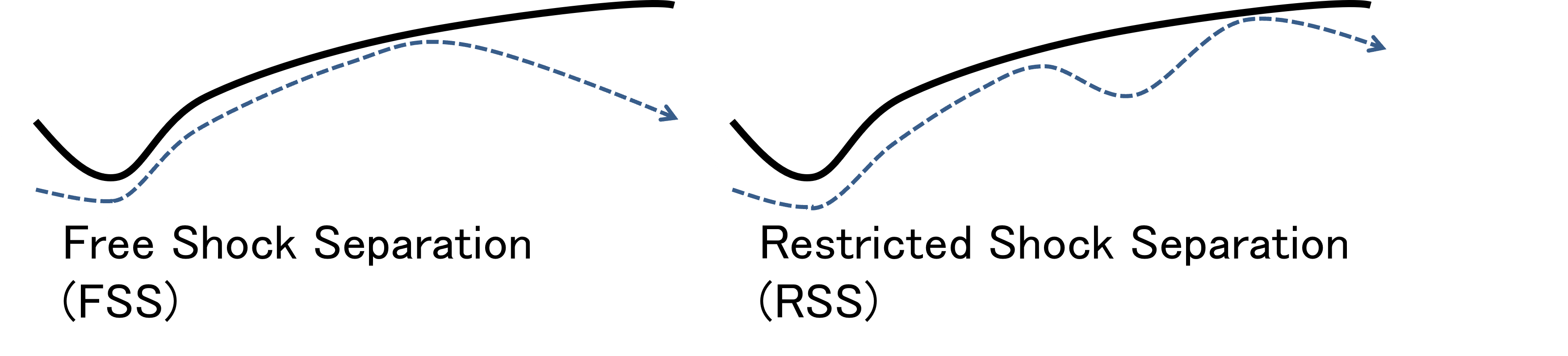 Figure 1. ノズル内部に発生するはく離流れの形態 | |||||||||
| 目的 |
以上に述べたノズル内部のはく離により,横力が発生しノズル全体の振動や推力低下に繋がると考えられている.
ノズル内部において流れがはく離することなく外部に流出することができれば,横力の抑制や推力の向上を期待できる.
そこで,ノズル内部のはく離の抑制を目的としてExpansion-Deflection(E-D)ノズルを改良した新型ロケットノズルの開発を検討する.
E-Dノズルは図2に示すようなノズルで,ノズルスロート部のセンターボディにより流れを偏向,膨張させることにより推力を得るという仕組みである. 新型ノズルでは,図3に示すようにセンターボディの代わりに噴射管を設置する. 噴射管から圧縮空気を吹込むことで,ノズル内部の流れを壁面に押し付けてはく離を抑制するという仕組みである. 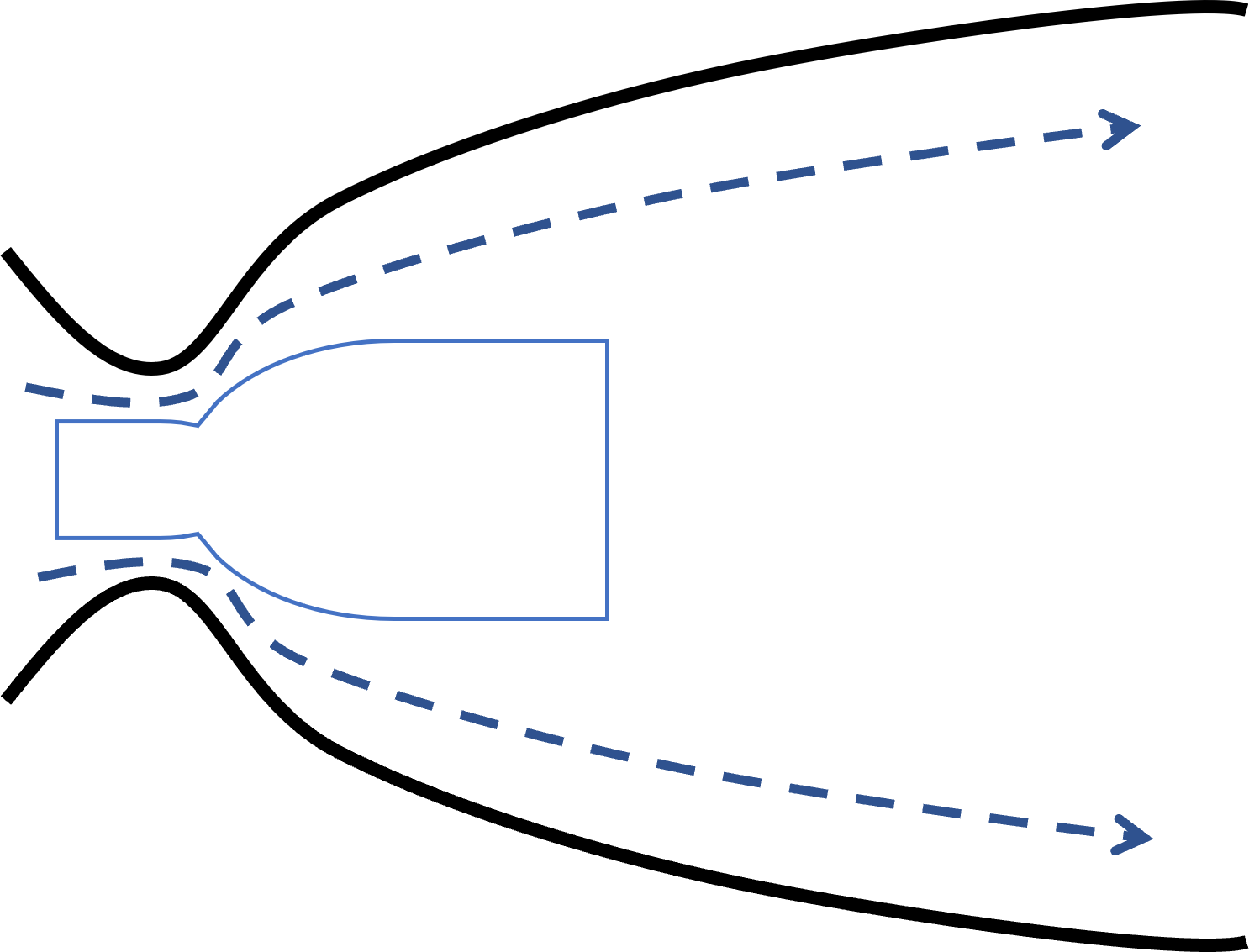 Figure 2. E-Dノズル 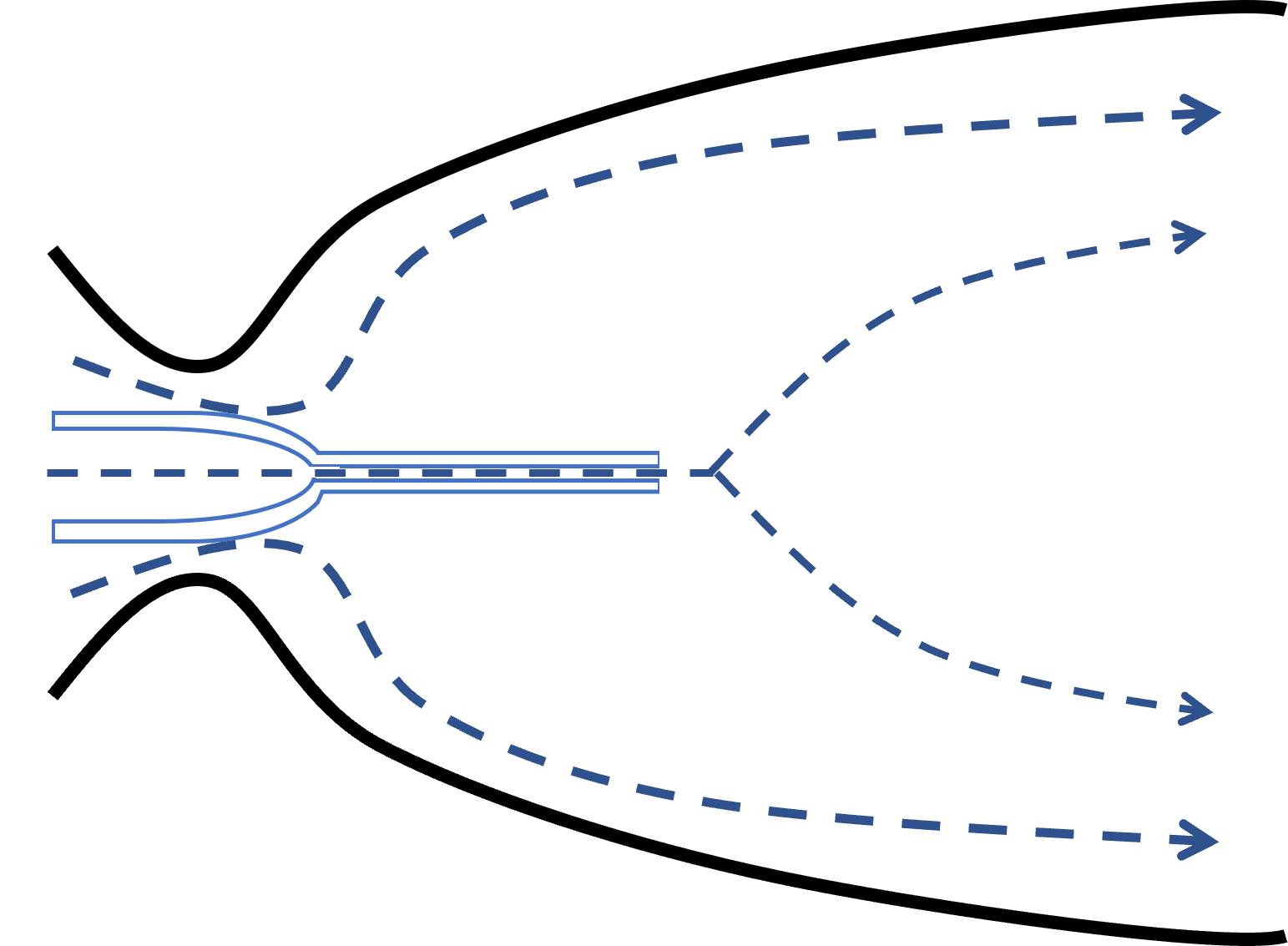 Figure 3. 噴射管を設置した新型E-Dノズル | |||||||||
| 方法 |
噴射管を設置するにあたり,二次元定常状態(ⅰ)および二次元非定常状態(ⅱ)における数値計算を行うことで,一般的なベル形ノズルの内部において流れ場にどのような変化が生じるのか比較検討する.
計算に用いた軸対称ノズルは特選曲線法を用いて設計し,出口マッハ数6.0,スロート径および出口の断面積比を49とした.
数値計算で用いたノズルを図4に示す.
いずれの数値計算についても熱流体解析ソフトウェアANSYS FLUENT 2020R2を使用する. Figure 4. 使用したノズル ⅰ. 流れは二次元定常流として,支配方程式は圧縮性Navier-Stokes方程式をk-εモデルを用いて解いた. 低高度での飛行を想定しているため,背圧は大気圧(101kPa)で固定した.入口圧を変化させることによりノズル圧力比NPR(入口圧/背圧)をそれぞれ24,27,36とした. ⅱ. 流れは二次元非定常流として,支配方程式は圧縮性Navier-Stokes方程式をSpalart-Allmarasモデルを用いて解いた. 設定した全圧および全温の最小値・最大値,また上昇速度は表1のとおりである. またタイムステップ数は20000とし,タイムステップサイズを0.0005sとした.
| |||||||||
| 結果 |
ⅰ. 図5から図7にNPR=25,27,36の場合における定常計算の結果を示す.上側にマッハ数分布および流線,下側に圧力分布を表した.
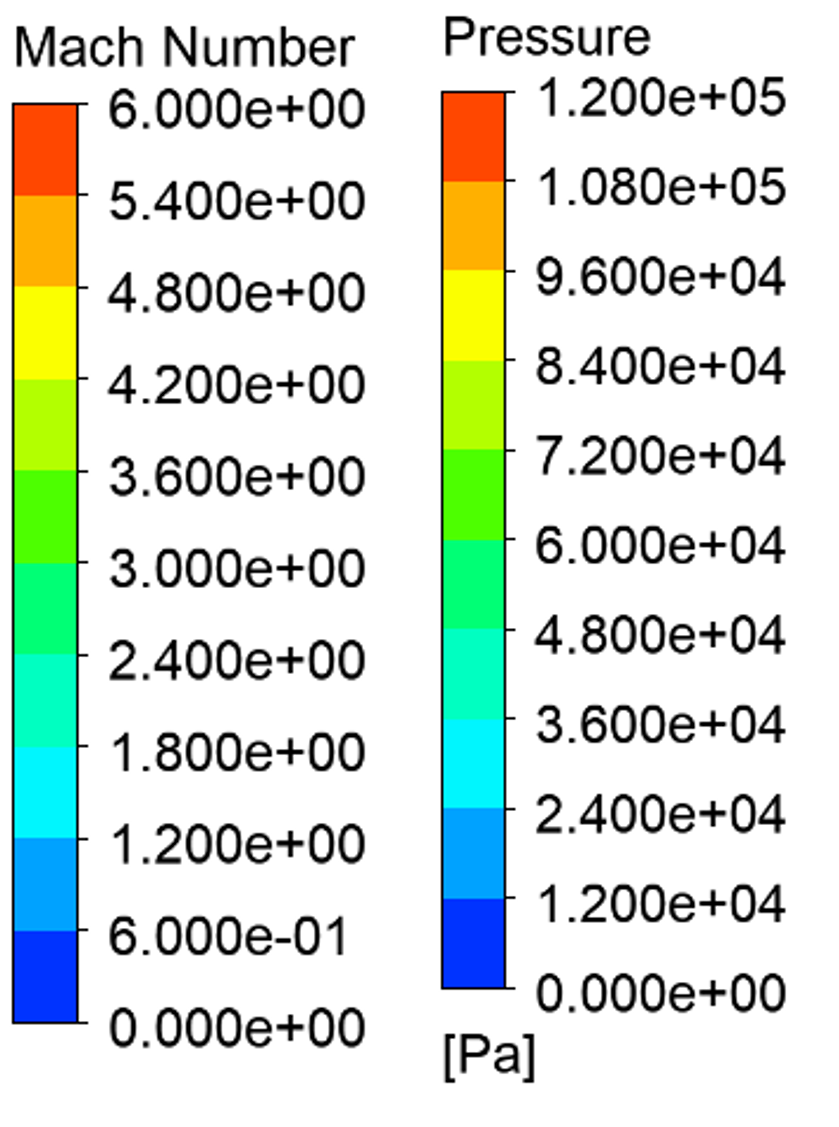  Figure 5. NPR=25. 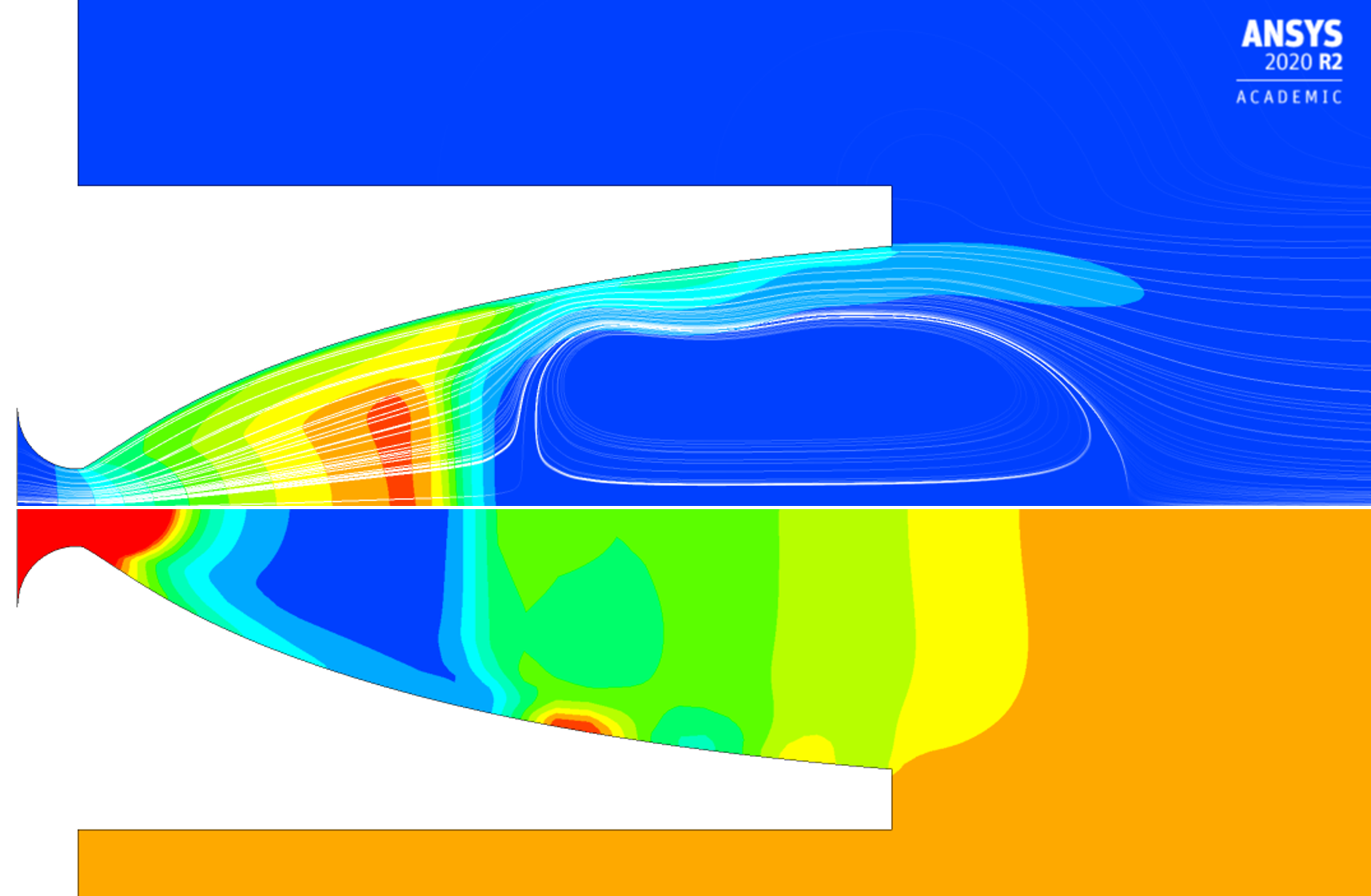 Figure 6. NPR=27. 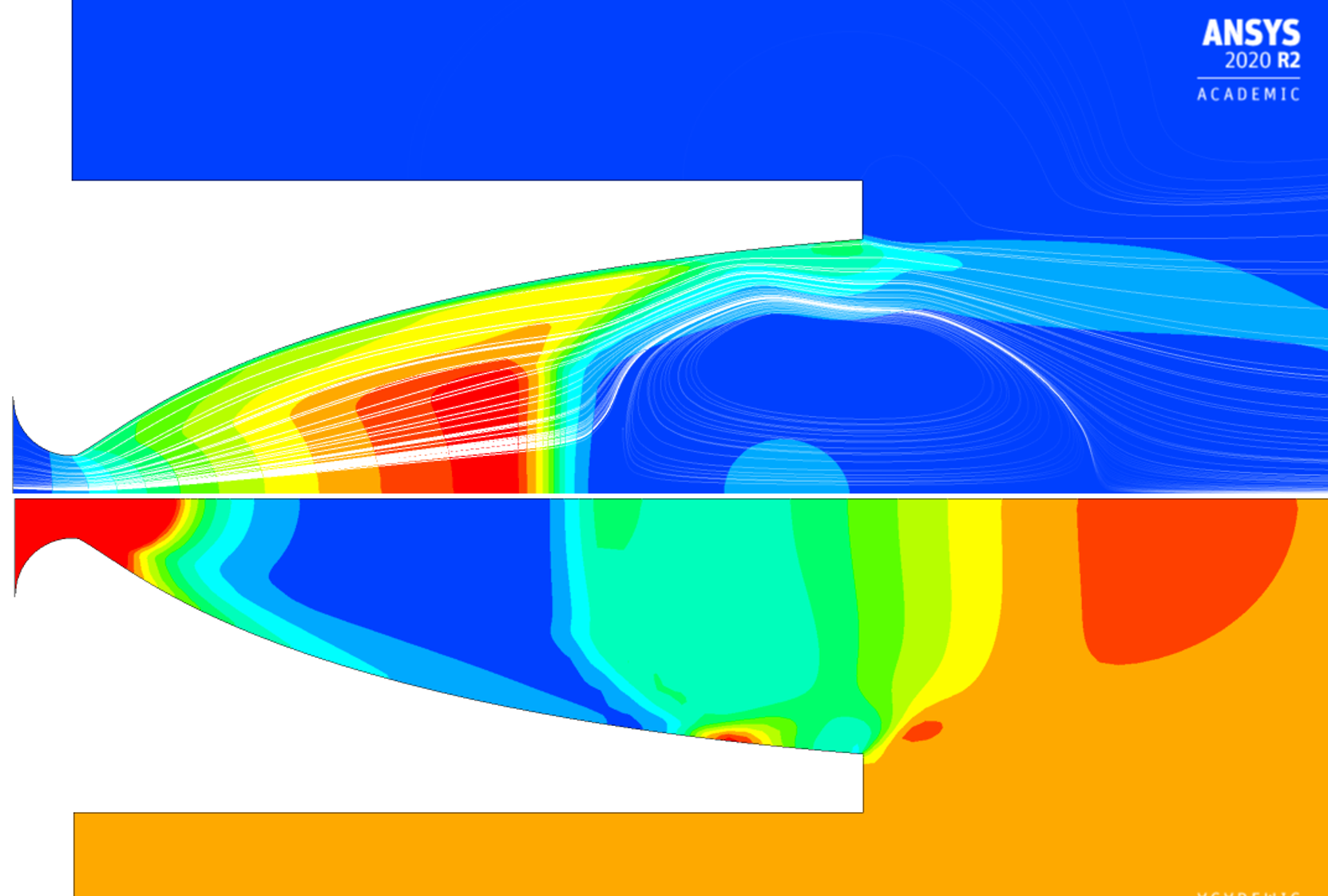 Figure 7. NPR=36. 図5より,ノズル壁面においてはく離した流れが再付着する様子が見られた. RSSが発生していることがわかり,ノズルの軸側には渦輪が発生している. 同様に図6においてもRSSが発生し,軸側に渦輪が発生していることがわかる. マッハ数分布および圧力分布についても,NPR=25の場合とNPR=27の場合に大きな差は見られなかった. 図7において,図5および図6の場合にみられたはく離の再付着点が下流に移動し,FSSが発生していることがわかる. はく離した流れは壁面に付着することなく出口から流出している. 以上より,NPR=27とNPR=36の間にRSSからFSSに遷移していることがわかる. ⅱ. 図8から図11に非定常計算の結果を示す.抽出したNPRはNPR=24,27,36,68とした.   Figure 8. NPR=24.  Figure 9. NPR=27.  Figure 10. NPR=36. 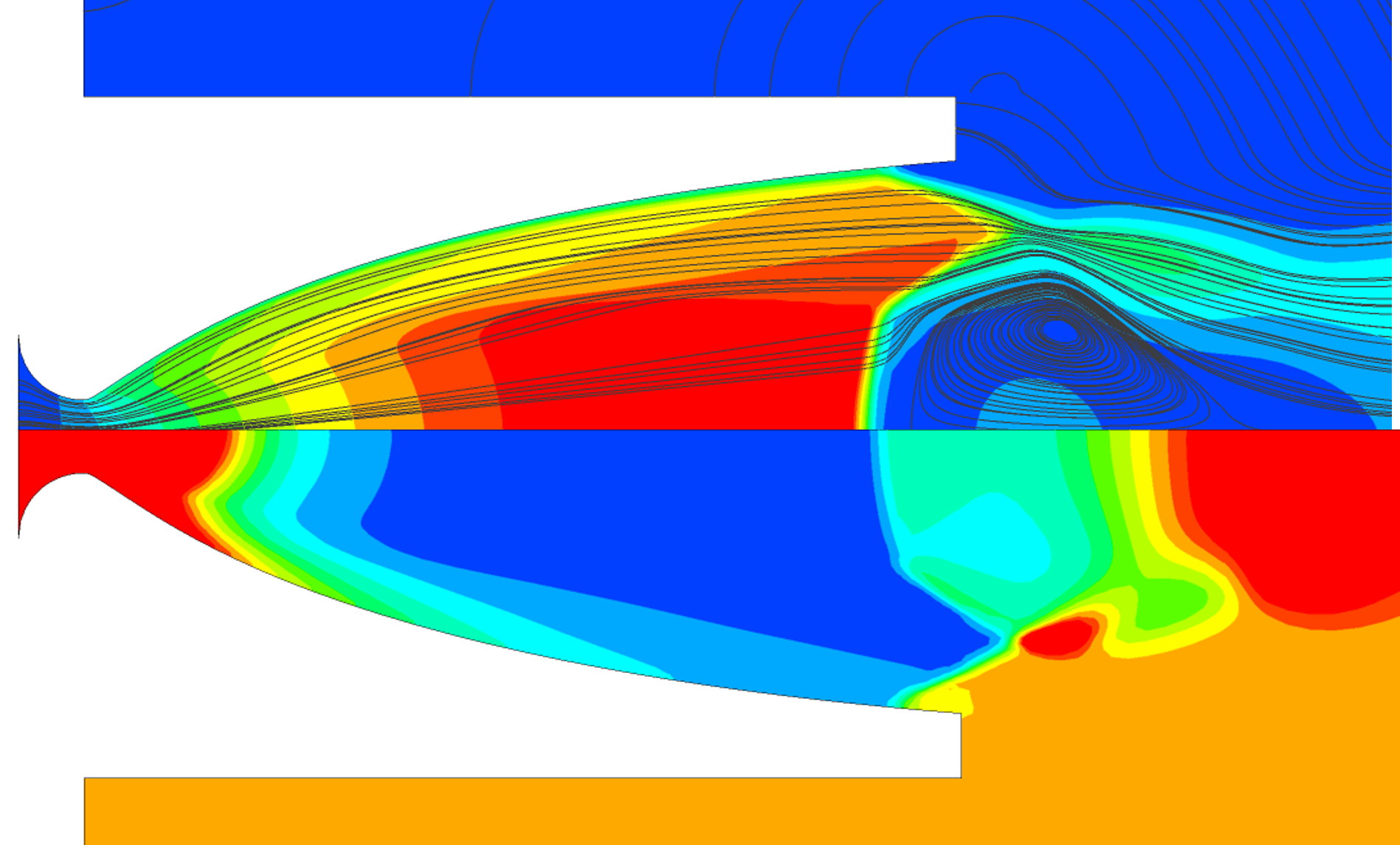 Figure 11. NPR=68. 図8より,ノズル壁面においてはく離した流れが再付着する様子が見られた. RSSが発生していることがわかり,ⅰ同様,軸側において渦輪が発生した. 図9において,図8で見られたはく離点が下流に移動していることがわかる. 壁面におけるはく離点および再付着点の距離が近くなったがRSSの発生は変わらず,圧力分布に至っても大きな変化は見られなかった. 図10では,図9で見られたはく離点が更に下流に移動し,流れが再付着することなく出口から流出していることがわかる. 渦輪は壁面の付近で見られ,FSSが発生しているとわかる. 図11では,はく離点が下流付近にあり,はっきりとしたFSSを観測することができた. 出口における圧力分布およびマッハ数分布から,はく離の影響による推力の低下が予想される. 以上の計算結果より,定常計算および非定常計算においてFSSやRSSの発生条件に大きな差は見られなかった. また,いずれにおいてもNPR=27からNPR=36の間にRSSからFSSに遷移していることがわかった. 今後は上記のNPRの範囲に着目し,噴射管を設置したノズルを設計して数値計算を行うことで,はく離抑制の効果を検証する. |