| 課題 | 貫流羽根車を回転させた際の偏心渦の旋回過程 | ||||||
| 背景 |
図1のような貫流羽根車を回転させると,図2のように内部で偏心渦が旋回する.偏心渦は周期的な旋回をするが,その周期性のために振動,騒音を発生させると考えられている.また,内部の流れは極めて複雑であるため,今日でもファンの設計は経験則に頼ることが大きく,昨今のさらなる小型化・薄形化ならびに低騒音化の要求にこたえるためには系統的な知見が必要である.
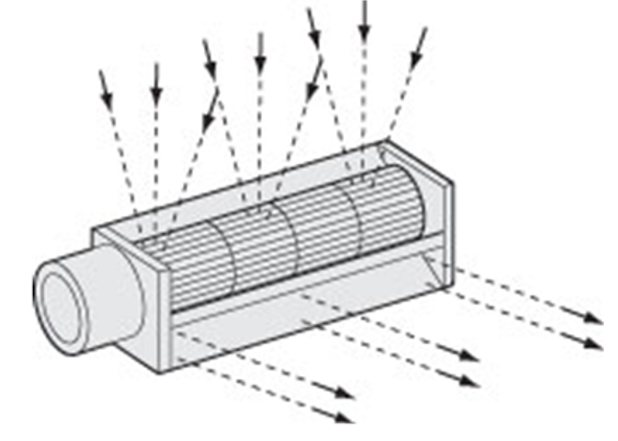 Figure 1. 貫流羽根車. 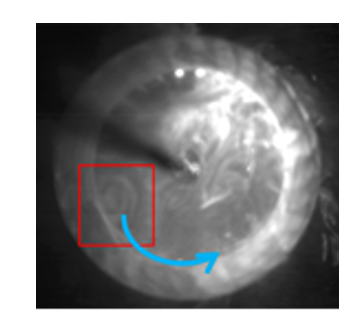 Figure 2. 偏心渦の旋回. 目的 |
穴口らの先行研究において,アスペクト比と境界条件が与える旋回への影響を,流体の流速や,波形からFFTで得たスペクトルピーク,偏心渦の位相遅れの観点から研究している. ただし,偏心渦や流れ場の様子をわかりやすく捉える渦度については,研究の標本数において十分に考慮されておらず未達状態にあり,より深い検討の余地がある.これは,山口らや穴口らによって,偏心渦が旋回することで振動,騒音の発生に至ると考えられており,渦度の様子を観察することや上下境界,アスペクト比を変化させることで,振動の原因となる偏心渦の旋回の速度や方向を調べることができるためである.また,半径方向の渦度に加え,翼方向の渦度も考慮することで,多角的に渦度と流れ場の旋回への影響を検討する.そして,本研究では,偏心渦の旋回のメカニズムを知る基礎研究であるとともに,計算と実験の簡略化を図り,流れ場の鏡像の関係の是非の確認も行う.
したがって,本実験では,偏心渦の旋回メカニズムの解明にむけ,上下境界とアスペクト比が偏心渦の旋回に与える影響を知るために,鏡像の関係性を確認しながら,壁面の境界条件を変えて,半径方向,軸方向の渦度や,旋回の周期性や変化を比較し調べることを目的とする.また,時刻遍歴に伴う偏心渦の成長を可視化や循環による定量化により観察,評価する.
| 方法 |
本研究では,偏心渦の成長過程を実現象として捉え,その旋回メカニズムを調べるため,下壁面を設け,偏心渦の可視化実験を行った.測定箇所はミドルスパンとした.実験装置の概要を図3に示す.
以下に実験手順を記す.
(1) スモークワイヤに発煙材を塗布し,ファン底部中心にあけた窪みにワイヤ先端が入るよう固定する.
(2) ファン内部に煙が充満させる.
(3) モータ電源といれ,ファンを回転させると同時に,録画をする.
| 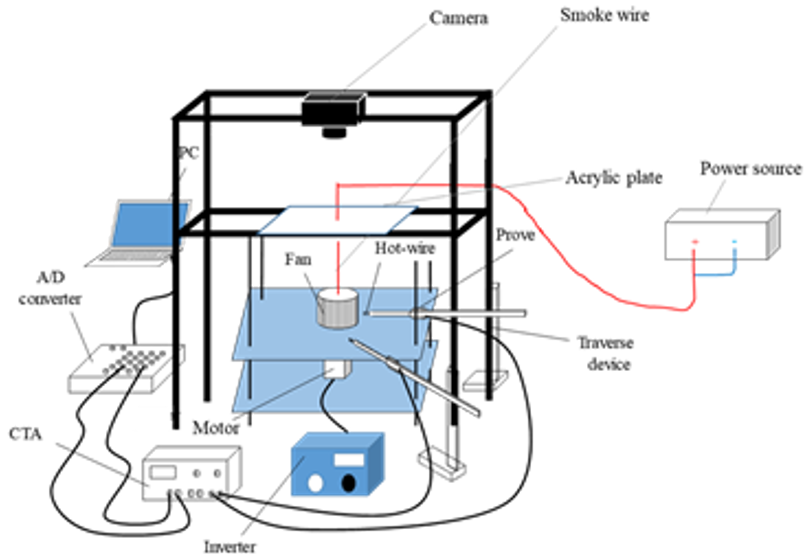 Figure 3. 実験機概要. 数値計算には熱流体解析ソフトウェアANSYS CFX 2019 R2を使用した.支配方程式は,非定常非圧縮Navier-Stokes方程式である.図4,5に計算領域,表1に羽根車の諸元を示す.計算領域は,ファンの中心軸に対し,軸対称とした.図4のように,下壁面のみ設置した場合と,図5のようにファン周囲に壁面設けない場合の計算を行った.下壁面を設置した場合のアスペクト比を1とし,壁面を設置しない場合のアスペクト比を2とした.下壁面のみの計算領域は,半径方向に羽根車直径の10倍,翼方向に翼高さの10倍とした.境界条件は,図4に黄色で示す境界を大気開放とし,青で示す下壁面を滑り壁面,その他の面を滑りなし壁面とした.壁面無しの場合は,翼方向高さを翼の19倍とした.境界条件は,図4と同様に,黄色で示す境界を大気開放,その他の境界を滑りなし壁面とした. 羽根車回転数はfn=17Hzとした.乱流モデルはk-εを使用した.時間刻みは1ステップあたり羽根車が1/4翼間回転する時間とした. 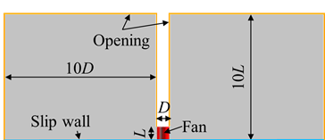 Figure 4. 滑り壁面. 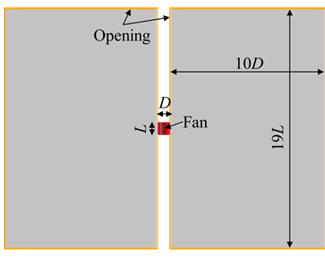 Figure 5. 滑りなし壁面. 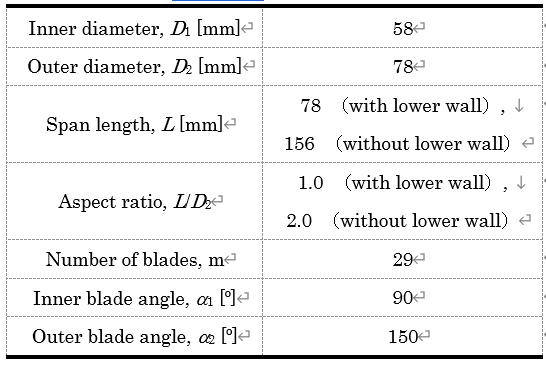 結果 |
図7~12は,アスペクト比L/D2=0.35の羽根車を回転させた際の煙の時間変化を示している.図7よりファンは旋回を始めた.図8において,すなわちファン旋回から0.0080秒後に,ファン内部の翼の末端付近から渦が生まれた.赤枠は発生点を示す.その後,図9の赤枠内に示すように,偏心渦は渦巻いた形状になりつつ,ファンの回転方向と同期した前周り旋回をしていることがわかった.ただし,図10を境に,偏心渦は翼間に入り込むように移動し,翼内部で旋回するようになった.図11では,偏心渦の形を崩すようになり,翼内部でより大きな渦を形成するとわかった.最後に,図12からは,偏心渦の形状や大きさをほとんど一定に維持したまま旋回し続けることがわかった.また,赤枠に示すように,ファン外部に吐出し領域が確認されるようになった.
|  Figure 7. r=0.248s. 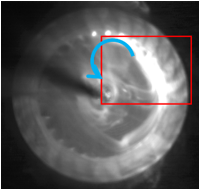 Figure 8. r=0.328s. 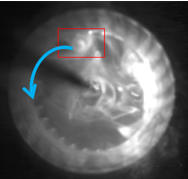 Figure 9. r=0.368s. 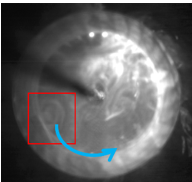 Figure 10. r=0.408s. 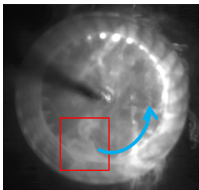 Figure 11. r=0.428s. 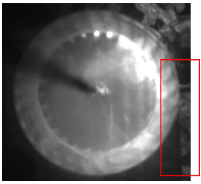 Figure 12. r=0.528s. 図13に,流速波形をFFT解析にかけた際の,各周波数のスペクトルピークを示す.横軸は無次元周波数f/fnを示す.縦軸は無次元速度を示す.vは計測した流速を示す.uは羽根車の周方向速度を示す.fはFFT解析したときのそれぞれの波の周波数を示す.計算上の計測箇所は,下壁面のファン中心から軸方向に39mm,半径方向に49mmの箇所である.図13より,周期波形のFFT解析から,ファンの回転周波数fn=17Hzとは異なる偏心渦旋回のピークが見られた.また,同じf/fn=0.056において,最も大きな値でのスペクトルピークをとることがわかった.このことから,L/D2=1.0,滑りあり壁面の条件と,L/D2=2.0,壁面なし条件は周期性において一致しているといえる. 図14に,図13で得られた,無次元周波数f/fn=0.05のスペクトルピークでの位相差を示す.横軸は計測点角度差であり,縦軸は位相差である.計測箇所は,下壁面のファン中心から軸方向に39mmの点を中心に,半径方向に49mmの点を10°毎として,一周分36か所である.図13より,いずれも単調増加するグラフであることがわかった.また,いずれの位相差を測定角度差で除した勾配も,ほぼ等しい値を示していることがわかった.さらに図14より,計測点角度差が360°の際に位相差が360°となっていることから,1セルの旋回であることが判明した.加えて,角度差がファンの回転方向に拡大していくたびに,位相差が正の値を保ちながら増加していることが判明した.これは,位相進みが発生しているため,セルがファンの回転方向と逆方向に回転していることを示している.以上より,1セルが後周りに旋回していることが明らかになった. 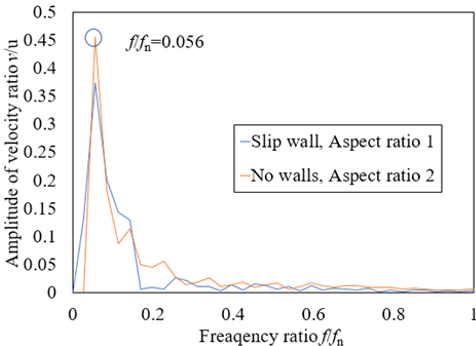 Figure 13. FFTスペクトル. 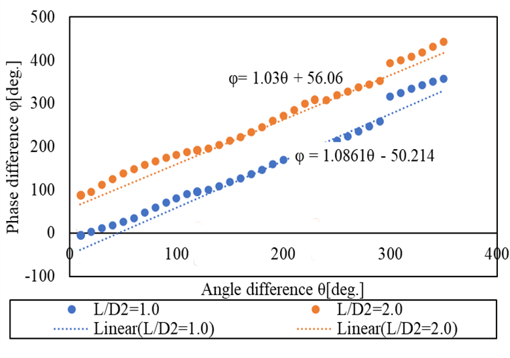 Figure 14. 位相差. 図13と図14の結果より,スペクトルピークや,偏心渦の旋回方向,旋回の周期性における一致を確認することができたが,壁面なしの条件では,上下対称の吐き出しであったため,図15に示す鏡像の関係に当てはめることができる.鏡像の関係では,図15において,点Aに強さqの吹き出しまたはΓの渦点が置かれている際,点Bに強さqの吹き出しまたは-Γの渦点を置くことにより,x軸を壁(Ψ=一定)と考えられる.この関係から,壁面のない条件L/D2=2.0と滑り壁面条件L/D2=1.0の流れ場は対応すると考えられる.これは図16の壁面滑りの是非が渦度に与える影響の比較からもわかる.図16(a)の,枠で囲まれた滑りなし壁面の下壁面付近では,左回りの渦を確認できる.一方で,図16(b)の滑り壁面について,吐出し領域が下壁面左側付近に確認できる.これは,壁面なしアスペクト比2の流れ場に同様である.以上の比較より,滑り壁面でこそ,鏡像法より,壁面なしでアスペクト比が2倍の流れ場を再現できる.これを踏まえ,図17~20で滑りなし壁面としたアスペクト比L/D2=1.0と,滑りあり壁面アスペクト比L/D2=1.0を比較し,鏡像の関係性が成立することを実証する. 図17~20は,半径方向と翼方向のそれぞれの断面における渦度を示しており,鏡像の関係と比較して,下壁面を設けたL/D2=1.0と壁面のないL/D2=2.0の条件の流れ場の一致を確認する.zu 17の L/D2=2.0,壁面のない条件の場合,下壁面の円の中心から軸方向に79mmの点での断面と,図18の L/D2=1.0,滑りあり壁面の場合の,下壁面の円の中心から軸方向に39mmの点での断面である.図19,20の断面は,円の中心を通る翼方向のA-A’断面を示す.図19の L/D2=2.0,壁面のない条件と図20の L/D2=1.0,滑りあり壁面は,いずれもファン周囲に偏心渦を伴い,偏心渦から流線が伸びているのを確認できる.旋回方向前面の橙色の枠内には吐き出し領域が確認でき,旋回する偏印渦の後面の黄色の枠内には翼からの剥離が見られる. また、鏡像の関係より,図19の L/D2=2.0,壁面なし条件の上半分の領域と,図20の L/D2=1.0,滑りあり壁面は,上壁面周辺や中心部分において,ファン周囲に伴う偏心渦の様相に類似性が見られる.図20は,水平線の軸について,上下対称に構成されている.流線については,いずれも,上壁面付近で円弧を描くようにしており,ファンの中心部分に流線が収束していることが確認できる.渦度については,赤で示された偏心渦の位置より同等といえよう.よって図19,20より,L/D2=2.0,壁面なし条件の上半分の領域と, L/D2=1.0,滑りあり壁面は,渦度,流線,吐出し領域や剥離において,同程度の流れ場を再現できた.さらに,鏡像の関係より,任意のアスペクト比の組においても,流れ場の類似性を作り出すことができると考えられる. 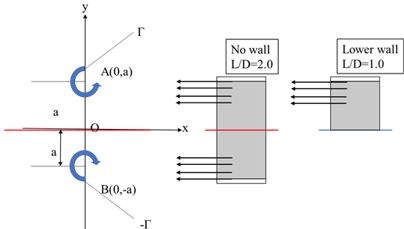 Figure 15. 鏡像の関係.  Figure 16. 壁面条件による違い. 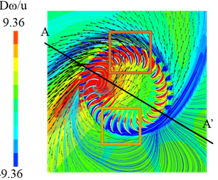 Figure 17. アスペクト比2,壁面なし.  Figure 18. アスペクト比1,滑り壁面. 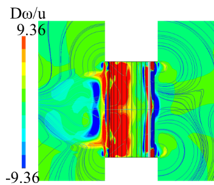 Figure 19. アスペクト比2,壁面なし. 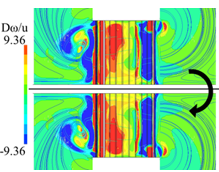 Figure 20. アスペクト比1,滑り壁面. |